|
[教学目标]
1.会按三角边的大小关系对三角形进行分类。
2.会阐述三角形三边关系定理及推论。
3.会应用三角形三边关系定理及推论判断三条线段能否组成三角形。并能根据三角形中已知两边的长,求第三边长的范围。
此外,通过列方程组求三角形边长,从中渗透“方程观点”,培养学生把实际问题转化为用方程(组)来求解、研究几何问题用代数列方程(组)来解题的意识。
[引导性材料]
三角形的三条边是否相等有多少种可能情况?请你画出各种可能情况。
说明:这里设计思考问题并画图,实质培养学生能自觉地借助形象思维实现抽象思维,逐步使两种思维得到协调的发展。
[教学设计]
问题1:在上述所画各种可能情况的三角形中,指出你所学过的三角形。
上述所画各种三角形中,大家已熟知的有等腰三角形和等边三角形,还有一种叫“不等边三角形”。
问题2:怎样的三角形叫等腰三角形?怎样的三角形叫等边三角形?
问题3:你能仿照“等腰三角形”的定义阐述怎样的三角形叫不等边三角形吗?
生活中常常不十分严格的区分“有”和“只有”的含义。比如“教室里有一个学生”与“教室里只有一个学生”常被理解为相同的意思。教学语言与生活语言既有联系,也有区别。比如教学中“有两条边相等的三角形”与“有且只有两条边相等的三角形”的意义不相同。“有两条边相等的三角形”包括“有且只有两条边相等的三角形”以及“三边都相等的三角形”两种情况。
问题4:如果把三角形按边的相等关系分类,现在你认为怎样分类恰当?
说明:设计问题4,让学生在主动寻找三角形按边的相等关系如何恰当的分类中,了解正确地对事物进行分类,必须将讨论的对象不重复不遗漏地分成若干种情况。
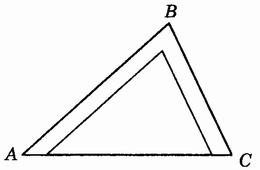
图3.2-1
问题5:如图3.2-1,由A经B到C是一条柏油路,AC是一条小路。人们从A步行到C,通常不走柏油路,而走小路,你能用你学过的知识来解释这种生活现象吗?由此你发现△ABC三边之间有大小关系吗?有怎样的大小关系?
问题6:请你根据不等式AB+BC>AC
AB+AC>BC、BC+AC>AB,用文字语言概括三角形三边的关系。
问题7:不等式AB+BC>AC、AB+AC>BC、BC+AC>AB,揭示了三角形三边关系定理“三角形两边的和大于第三边”,根据这三个不等式还可以推得推论“三角形两边的差小于第三边”。你能推证这个推论吗?
推论是由定理直接推出的结论,和定理一样可以作为进一步推理的依据。
[例题解析]
例1:下列长度的三条线段能否组成三角形?为什么?
(l)3cm,4cm,5cm;(2)5cm,6cm,11cm;
(3)5cm,6cm,10cm。
说明:1.本例是课本第10页练习第1题。
2.本例的解答中,要引导学生认识判断三条线段能否组成三角形,必须检查三条线段中任何两条的和是否都大于第三条。进而学生易于发现简便的判断方法──满足较小两条线段之和大于第三条线段,便可构成三角形。
例2:(即课本本节例题)
说明:1.通过本例使学生了解几何中常常利用代数列方程的方法解题。
2.本例计算虽较简单,但思维能力的要求较高。既要对已知边的可能情况分类计算,又要考虑求解结果是否满足三角形三边关系定理。
由于不少学生习惯于代数学习中套用方程式的学习方法面对几何学习,不注重形象思维,更不会形象思维的同时使用抽象思维。因此本例的教学应把侧重点放在引导学生自己去探索,帮助他们克服思维不严密、套用方程式的学习习惯。
例3:△ABC中,已知a=8cm,b=5cm,能确定c边的长度吗?能确定c边的长度范围吗?
说明:本例的教学中要引导学生认识:(1)本例中要求一个未知量(C边的长度),但是没有给出与C边有关的相等关系,所以未知数的个数大于相等关系个数,故本例有无数个解,即C边的长度无法确定。
(2)由于三角形的三边有特殊的大小关系,因此根据三角形三边关系定理及推论可以确定C是大于3且小于13范围内的无数个值。
[课堂练习]
2.(补充练习)已知三角形的两边的长分别是4cm和7cm:
(l)如果这个三角形是等腰三角形,求这个三角形的周长;
(2)如果第三边长的数值是偶数,求这个三角形的周长。
[小结]
1.从三角形三边关系的研究中可知三角形的三边相互制约──任意两边之和大于第三边,且任意两边之差小于第三边。
2.判断a、b、c三条线段能否组成一个三角形,应注意a+b>c、a+c>b、b+c>a三个条件缺一不可。当a是a、b、c三条线段中最长的一条时,只要b+c>a,就有任意两条线段的和大于第三条。
3.为了研究方便,几何中常常把图形进行分类。由于三角形有边和角两类元素。所以三角形通常按边的相等关系分类和按角的大小关系分类。后面的学习中我们还要研究三角形按角的大小的分类。
[作业]
课本习题3.IA组第6、7、8、9题。
| 
