|
教学目标
1.会说出二元一次方程、二元一次方程组的意义,会判断一个方程(组)是不是二元一次方程(组)。
2.会说出二元一次方程组的解的意义,会检验一对数是不是二元一次方程组的解。
此外,借助实际问题中“相等关系个数、未知数个数以及问题的解的个数”的探究,从中渗透“方程观点”,逐步培养学生把实际问题转化为用方程组来求解的意识。
引导性材料
(教科书提供了一个引导性材料,这里另外给出一个引导性材料,提供课堂教学中参考。)
已知甲、乙骑自行车同时从相距60千米的两地相向而行,经过2小时相遇,你能求甲、乙两人的速度吗?
(对引导性材料中提出的问题,学生经过短时间的思考,常有两种不同的意见,大多数学生认为这个问题无解;少数学生认为这个问题的解不能确定,有许多种可能情况。)
知识产生和发展过程的教学设计
问题1 你认为上述问题有没有解?有多少解?如果你认为有许多解的话,试举几个解。
问题2 请你改编上述问题,使问题有确定的解,并列一元一次方程求出问题的解。
(如果学生不能在课堂上短时间内改编问题,教师可以准备好1—2个改编的问题,提供学生借鉴,例如
问题l—l 甲、乙骑自行车同时从相距60千米的两地相向而行、经过2小时相遇,已知乙的速度是甲的速度的2倍。求甲、乙两人的速度。
解:设甲的速度为x千米/时,则乙的速度为2x千米/时。
根据题意,得2(x+2x)=60
解得 x=10
∴ 2x=20
答:甲的速度为10千米/时,乙的速度为20千米/时。
问题l—2 甲、乙骑自行车同时从相距60千米的两地相向而行,经过2小时相遇,已知甲的速度是乙的速度的2倍,且乙每小时比甲每小时多走2千米。求甲、乙两人的速度。
对于问题1-2,学生立即就能判断这个问题无解。
问题3 根据上面的研究,请你填写下表,从中你发现相等关系个数、未知数个数、解的个数之间有联系吗?有什么联系呢?这些联系是必然的吗?还有没有其他情况?
|
相等关系 |
未知数个数 |
解的个数 |
用方程表示相等关系(设甲的速度为x千米/时,乙的速度为y千米/时) |
| 问题1 |
(1)(甲速+乙速)×2=60。 |
2 |
无数 |
2(x+y)=60, |
| 问题1-1 |
(1)(甲速+乙速)×2=60,
(2)乙速=甲速×2。 |
2 |
1 |
2(x+y)=60,
y=2x。 |
| 问题1-2 |
(1)(甲速+乙速)×2=60,
(2)乙速=甲速×2,
(3)乙速-甲速=2。 |
2 |
0 |
2(x+y)=60,
x=2y,
y-x=2。 |
问题4 上表中的方程都叫二元一次方程,你认为什么样的方程才能叫二元一次方程?请在下列说法中指出恰当的说法来。
(l)含有两个未知数的方程叫二元一次方程。
(2)含有两个未知数,并且来知数的次数是1的方程叫二元一次方程。
(3)含有两个未知数,并且未知项的次数是1的方程叫二元一次方程。
上表中,根据问题1一1所得的两个方程中的未知数x,都表示甲的速度;未知数y,都表示乙的速度。我们把这样的两个方程,用一个大括号合在一起,就组成了二元一次方程组。
问题5 从上面列一元一次方程求解问题1—l中;你发现方程组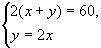 的解是什么? 的解是什么?
一般地,使二元一次方程组的两个方程左、右两边的值都相等的两个未知数的值,叫做二元一次方程组的解。
(说明:1.由于学生习惯于小学算术学习中一个问题只有一个解,因此常常认为问题没有确定的解就是问题无解。通过对问题1的讨论,初步渗透“函数思想”。
2.对问题1进行改编,实质是渗透“方程观点”,这种探讨对学习二元一次方程组的有关概念,似乎没有明显的联系,其实这种训练使学生从另一个角度深化了对二元一次方程组的概念的理解。爱动脑子的学生会想到“三个二元一次方程组成的方程组叫不叫二元一次方程组?为什么教科书研究由两个二元一次方程组成的方程组?”这里通过对问题1进行改编,不仅起到“释疑”的作用,而且有助于培养学生用较高层次的观点,即问题中相等关系个数、未知数个数与问题解的个数三者间的关系来审视、研究问题,为后续一次方程的应用、待定系数法的教学作出铺垫。
例题解析
例1 (由教科书第6页练习1改编)已知下面三对数值:
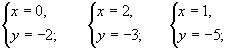
(1)哪几对使方程2x-y=7左、右两边的值相等?
(2)哪几对使方程x+2y=-4左、右两边的值相等?
(3) 哪一对是方程组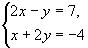 的解? 的解?
例2 已知满足二元一次方程组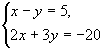 的x的值是-1,那么由此可以知道什么? 的x的值是-1,那么由此可以知道什么?
(说明:1.本例是根据教科书第8页A组第4(1)题改编。原题要求方程组的解,但学生常常有困难,因此这里把原题改为开放式命题,看起来似乎比原题的要求高了,其实有利于各类学生参与并寻求结论。
2.本例实质又一次培养学生运用“问题中相等关系个数、未知数个数与问题解的个数三者间的关系”来审视问题:方程组中每个方程虽都涉及两个未知数,但已知一个未知数x=l,因此实质每个方程都是含有一个未知数y的一元一次方程,所以求解其中任一个方程,就能求得y的值,于是就可得原方程组的解。)
课内练习 教科书第6页练习第2题。
教科书第7页习题5.1A组第1、2题。
小结
1“未知项的次数是1”是二元一次方程的意义的关键词语。
2.两个未知数的值合起来才是二元一次方程组的完整的解。要改变原有一个问题的解答通常是一个数值的思考习惯。
3.求两个未知数的问题,必须有两个独立的(不重复、不矛盾)相等关系,问题才有唯一确定的解。
作业 教科书第7页习题5.1A组第3、4(2)题,B组第1题。 | 



