第一课时
(一)教学过程
【复习提问】
1.分式的定义?
2.分数的基本性质?有什么用途?
【新课】
1.类比分数的基本性质,由学生小结出分式的基本性质:
分式的分子与分母乘以(或除以)同一个不等于零的整式,分式的值不变,即:
![]() ,
,![]()
(其中![]() 是不等于零的整式.)
是不等于零的整式.)
2.加深对分式基本性质的理解:
例1 下列等式的右边是怎样从左边得到的?
(1)![]() ;
;
由学生口述分析,并反问:为什么![]() ?
?
解:∵ ![]()
∴![]() .
.
(2)![]() ;
;
学生口答,教师设疑:为什么题目未给![]() 的条件?(引导学生学会分析题目中的隐含条件.)
的条件?(引导学生学会分析题目中的隐含条件.)
解:∵![]()
∴![]() .
.
(3)![]()
学生口答.
解:∵![]() ,
,
∴![]() .
.
例2 填空:
(1)![]() ;
;
(2)![]() ;
;
(3)![]() ;
;
(4)![]() .
.
把学生分为四人一组开展竞赛,看哪个组做得又快又准确,并能小结出填空的依据.
例3 不改变分式的值,把下列各式的分子与分母中各项的系数都化为整数.
(1)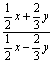 ;
;
分析学生讨论:①怎样才能不改变公式的值?②怎样把分子分母中各项系数都化为整数?
解: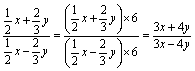 .
.
(2)![]() .
.
解:![]() .
.
例4 判断![]() 取何值时,等式
取何值时,等式![]() 成立?
成立?
学生分组讨论后得出结果:
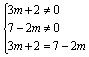 ∴
∴![]() .
.
(二)随堂练习
1.当![]() 为何值时,
为何值时,![]() 与
与![]() 的值相等()
的值相等()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.若分式![]() 有意义,则
有意义,则![]() ,
,![]() 满足条件为( )
满足条件为( )
A.![]() B.
B.![]() C.
C.![]() D.以上答案都不对
D.以上答案都不对
3.下列各式不正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
4.若把分式![]() 的
的![]() 和
和![]() 都扩大两倍,则分式的值
都扩大两倍,则分式的值
A.扩大两倍 B.不变
C.缩小两倍 D.缩小四倍
(三)总结、扩展
1.分式的基本性质.
2.性质中的![]() 可代表任何非零整式.
可代表任何非零整式.
3.注意挖掘题目中的隐含条件.
4.利用分式的基本性质将分式的分子、分母化成整系数形式,体现了数学化繁为简的策略,并为分式作进一步处理提供了便利条件.
(四)布置作业
教材P61中2、3;P62中B组的1
(五)板书设计