 打印本文
打印本文  关闭窗口
关闭窗口 教学目标
1.掌握公倍数、最小公倍数两个概念.
2.理解求最小公倍数的算理,掌握用分解质因数求最小公倍数的方法.
教学重点
建立公倍数和最小公倍数的概念,掌握求两个数最小公倍数的方法.
教学难点
理解求两个数最小公倍数的算理.
教学步骤
一、铺垫孕伏.
1.导入:这节课我们开始学习有关最小公倍数的知识.
(板书:最小公倍数)
2.复习倍数的概念.
二、探究新知.
教学例1【演示课件“最小公倍数”】
例1、顺次写出4的几个倍数和6的几个倍数.它们公有的倍数是哪几个?其中最小的是多少?
4的倍数有:4、8、12、16、20、24、28、32、36……
6的倍数有:6、12、18、24、30、36……
4和6的公倍数有:12、24、36……
其中最小的一个是12.
1、学生分组讨论总结公倍数、最小公倍数的意义.
2、用集合图表示4和6的公倍数.
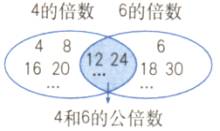
3、质疑:两个数的公倍数有什么特点?有没有最大的公倍数?
明确:因为每一个数的倍数的个数都是无限的,所以两个数的公倍数的个数也是无限的.因此,两个数没有最大的倍数.
4、反馈练习.
把6和8的倍数和公倍数不超过50的填在下面的空圈里,再找出它们的最小公倍数是几.
明确:50以内6和8的公倍数只有2个;如果扩展数的范围,也就是50以外6和8的公倍数则是无限的.
(二)教学例2【演示课件“最小公倍数”】
引入:我们用分解质因数的方法求两个数的最小公倍数.
例2:求18和30的最小公倍数.
1、用短除式分别把18和30分解质因数.
板书: 18=2×3×3
30=2×3×5
教师提问:18的倍数必须包含哪些质因数?
(18的倍数包含18的所有质因数)
30的倍数必须包含哪些质因数?
(30的倍数包含30的所有质因数)
18和30的公倍数必须包含哪些质因数?
(既要包含18的所有质因数,又要包含30的所有质因数)
2、观察集合图:18和30的最小公倍数应包含哪些质因数?
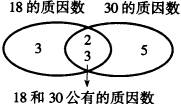
教师明确:18和30的最小公倍数里,只要包含它们全部公有的质因数(1个2和1个3)以及各自独有的质因数(3和5)就可以了.2×3×3×5=90,所以18和30的最小公倍数是90.
3、小组讨论:如果少一个或多一个质因数行不行?
教师明确:如果少一个质因数,就不能保证公倍数里包含18和30全部的质因数,因而就不能得到它们的最小公倍数;如果多一个质因数,虽是18和30的公倍数,但不能保证是最小公倍数.
板书:

18和30的最小公倍数是2×3×3×5=90
4、反馈练习.
(1)先把下面两个数分解质因数,再求出它们的最小公倍数.
30=( )×( )×( )
42=( )×( )×( )
30和42的最小公倍数是( )×( )×( )×( )=( )
(2)A=2×2 B=2×2×3
A和B的最小公倍数是( )×( )×( )=( )
(3)用分解质因数法求24和18的最小公倍数时,小华得72,小林得144.谁做错了?
可能错在哪里?
5、求最小公倍数的一般书写格式.
①引导学生把两个短除式合并成一个.
板书:

②明确:综合短除式中所有除数和商与18和30的最小公倍数90所包含的所有质因数是一一对应的,因此把短除式中所有的除数和商乘起来,就得到18和30的最小公倍数.
③反馈练习:求30和45的最小公倍数.
④总结方法:求两个数的最小公倍数,先用这两个数公有的质因数连续去除(一般从最小的开始),一直除到所得的商是互质数为止,然后把所有的除数和最后的两个商连乘起来.
⑤反馈练习:求下面每组数的最小公倍数
6和8 24和20 28和21 16和72
三、全课小结.
今天这节课我们主要研究了用什么方法求两个数的最小公倍数,它是为以后学习通分做准备的,希望大家能熟练的掌握这部分知识.
四、随堂练习【演示课件“最小公倍数”】
1.填空.
(1)A=2×3×5 (2)A=2×2×5
B=3×5×7 B=( )×5×( )
A和B和最小公倍数是( ). A和B的最小公倍数是2×2×5×7=140.
2.判断.
(1)两个数的积一定是这两个数的公倍数.( )
(2)两个数的积一定是这两个数的最小公倍数.( )
五、布置作业.
求下面每组数的最小公倍数.
12和15 30和40 36和54 22和33
六、板书设计.
最小公倍数
例1 顺次写出4的几个倍数和6的几个倍数.它们公有的倍数是哪几个?其中最小的是多少?
4的倍数有:4、8、12、16、20、M、28、32、36……
6的倍数有:6、12、18、30、30、36……
4和6公有的倍数有: 12、24、36……
其中最小的一个是12.
例2 求18和30的最小公倍数.

18和30的最小公倍数是 2×3×3×5=90.
探究活动
最小公倍数
活动目的
1、理解最小公倍数的意义.
2、培养学生良好的思维品质和科学的思维方法.
活动题目
有两个自然数,它们的最小公倍数是48,那么这两个自然数各是多少?
活动过程
1、学生分小组讨论.
2、小组汇报.
3、师生共同研究方法,理解求最小公倍数的几种情况.
参考答案
由题意可知,48是所求两个自然数的最小公倍数,那么所求两个自然数一定是48的约数,因此我们可以找出48的所有约数,然后进行两两组合,便可找出符合条件的数组.
48的约数有:1、2、3、4、6、8、12、16、24、48经试验,符合条件的数组有:1和48,2和48,3和16,3和48,4和48,6和16,8和48,12和16,12和48,16和24,16和48,24和48,48和48.一共有14个数组.
活动说明
学生寻找符合条件的答案的过程,实际上就是培养学生思维有序化的过程.
 打印本文
打印本文  关闭窗口
关闭窗口