1. 知识结构：

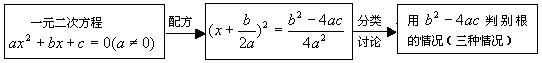
　　2. 重点、难点分析

　　（1）本节的重点是会用判别式判定根的情况.一元二次方程的根的判别式是比较重要的，用它可以判断一元二次方程根的情况，有助于我们顺利地解一元二次方程，也可以利用它进一步学习函数的有关内容，所以，它是本节课的重点.

　　（2）本节的难点是一元二次方程根的三种情况的推导.教科书首先将一元二次方程用配方法变形为 .因为，所以方程右边的符号就由来确定，而方程左边的不可能是一个负数，因此，把分三种情况来讨论方程根的情况.推导过程中利用了分类的思想方法，对于分类讨论学生感觉到较难，老师应该讲明分类的基本思想。

　　3. 教法建议：

　　（1）引入要自然、合理

　　新课引入前，作一个铺垫：前面我们讲了一元二次方程的解法，我们掌握了开平方法、公式法和因式分解法后，就可以解任何一个一元二次方程，但是，存在这样一个问题，并不是所有的一元二次方程都有解，我们可以通过把解求出来，来解方程，也可以通过判定方程无解，来解方程，这样我们就面临着一个问题，什么时候方程有解？什么时候方程无解？我们不解方程能不能判定根的情况？那就是我们本节所要研究的问题.让学生首先感觉到所要学习的知识并不突然，也显露了本节课的重点.

　　（2）利用多媒体进行教学

　　本节是根的判别式结论的推导，比较抽象，为了便于学生理解，使用所提供的动画，有助于学生对所讲内容的理解，调动学生主动思维的积极性，活跃课堂气氛，提高学习效率.

　　（3）本节在推导根的判别式的结论时，利用了分类的思想，对于学生这是一个难点，一定给学生讲清楚分类的依据，分类的基本思想，使学生对所得结论深信不疑.

一、教学目标

　　1. 理解一元二次方程的根的判别式，并能用判别式判定根的情况；

　　2. 通过根的判别式的学习,培养学生从具体到抽象的观察、分析、归纳的能力；

　　3．通过根的情况的研究过程，让学生深刻体会转化和分类的思想方法.

　　二、重点·难点及解决办法

　　1．教学重点：会用判别式判定根的情况。

　　2．教学难点：一元二次方程根的三种情况的推导.

　　3．解决办法：（1）求判别式时，应先将方程化为一般形式，确定a、b、c。（2）利用判别式可以判定一元二次方程的存在性情况（共四种）；方程有两个实数根，方程有两个不相等的实数根，方程有两个相等的实数根，方程没有实数根。

　　三、教学步骤

　　（一）教学过程

　　1．复习提问

　　（1）平方根的性质是什么？

　　（2）解下列方程：① ；② ；③ 。

　　问题（1）为本节课结论的得出起到了一个很好的铺垫作用。问题（2）通过自己亲身感受的根的情况，对本节课的结论的得出起到了一个推波助澜的作用。

　　2．任何一个一元二次方程 用配方法将其变形为 ，因此对于被开方数 来说，只需研究 为如下几种情况的方程的根。

　　（1）当 时，方程有两个不相等的实数根。

　　即

　　（2）当 时，方程有两个相等的实数根，即 。

　　（3）当 时，方程没有实数根。

　　教师通过引导之后，提问：究竟谁决定了一元二次方程根的情况？

　　答： 。

　　3．①定义：把 叫做一元二次方程 的根的判别式，通常用符号“ ”表示。

　　②一元二次方程 。

　　当 时，有两个不相等的实数根；

　　当 时，有两个相等的实数根；

　　当 时，没有实数根。

　　反之亦然。

　　注意以下几个问题：

　　（1） 这一重要条件在这里起了“承上启下”的作用，即对上式开平方，随后有下面三种情况。正确得出三种情况的结论，需对平方根的概念有一个深刻的、正确的理解，所以，在课前进行了铺垫。在这里应向学生渗透转化和分类的思想方法。

　　（2）当 ，说“方程 没有实数根”比较好。有时，也说“方程无解”。这里的前提是“在实数范围内无解”，也就是方程无实数根的意思。

　　4．例题讲解

　　例1  不解方程，判别下列方程的根的情况：

　　（1） ；（2） ；（3） 。

　　解：（1）

　　∴原方程有两个不相等的实数根。

　　（2）原方程可变形为

　　 。

　　 ，

　　∴原方程有两个相等的实数根。

此文章共有2页  第 1 2 页