教学设计示例1

　　课题：二次函数 的图象

　　教学目标：

　　1、会用描点法画出二次函数 的图象；

　　2、根据图象观察、分析出二次函数 的性质；

　　3、进一步理解二次函数和抛物线的有关知识

　　4、渗透由特殊到一般的辩证唯物主义观点；

　　5、渗透数形结合的数学思想方法，培养观察能力和分析问题的能力；

　　6、培养学生勇于探索创创新及实事求是的科学精神.

　　教学重点：根据图象，观察、分析出二次函数的性质

　　教学难点：渗透数形结合的数学思想方法

　　教学用具：直尺、微机

　　教学方法：谈话、探究式

　　教学过程：

　　1、列表、描点画出函数 与 的图象，引入新课

　　例：画出函数 与 的图象

　　解：列两个表

　　分别描点画图

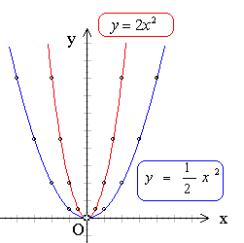
　　2、根据图象发现问题，由学生探索出新知识.

　　提问：你能从图象中发现抛物线是哪些性质？这两个函数图象有何异同？

　　（1）这两个函数的图象都关于y轴对称.这一点可以从刚才的列表中可以看出， 时所对应的y值分别相等，如 等.这样的两个点关于y轴对称.由这些点构成的抛物线也关于y轴对称.从解析式中也可以得出这个结论：互为相反数的两个数的平方数相等，因此，这两个函数的图象都是关于y轴对称的.

　　（2）从图中可以看出，x可取x轴上的任意一点，而y对应的是大于、等于零的数.即抛物线有最低点（0，0）.这一点可以从解析式中得到很好的解释， 可取

　　任意实数. 图象开口向上.这也说明数与形是数学中的两条线索，它们是互相对应的，反映了数形结合的思想.

　　（3）从图中也可以看出抛物线不同于我们以前学过的正比例函数和一次函数，这两个函数的图象都是直线，而抛物线是曲线，有一个拐弯，函数的图象都在最低点拐了一个弯.这样它们的性质几发生了变化.在y轴的左侧，从左向右呈下坡趋势，即y随x的增大而减小；在y轴的右侧，从左向右，呈上坡趋势，即y随x的增大而增大.这一变化趋势也可以从列表中看出.

　　（4）这两个图象除以上相同之处外，还有不同的地方.如： 离y轴近， 离y轴远.从列表中可以看出：如 过点（2，2），而 过点（2，8）也就是说，当x=2时， 的图象所对应的点高于 所对应的点.因此会有上述的结论.

　　3、画出函数 的图象

　　 与 中的a都是正数，当a<0时， 的图象会是什么样子呢？

　　我们看例2

　　例2、画出函数 的图象

　　解：列表：

　　描点画图：

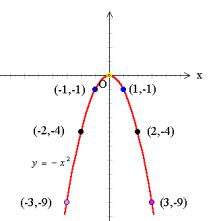
　　4、从函数图象入手，再次总结二次函数的性质

　　(1)与刚才两个图象不同的是， 的图象开口向下.这是因为x是任意实数， ， 即 ，因此，开口会向下.图象有最高点（0，0）

　　(2)此图象仍然是关于y轴对称的

　　(3)在y轴的左侧，y随x的增大而增大；在y轴的右侧，y随x的增大而减小

　　5、得出一般的规律

　　一般地，抛物线 的对称轴是y轴，顶点是原点，当a>0时，抛物线 的开口向上，当a<0时，抛物线 的开口向下，a的绝对值越大，图象越靠近y轴.

　　6、小结：这一节课，从始至中都是结合图象观察、归纳总结出二次函数 的性质，体现了数与形的结合.函数图象是解决函数问题的有利工具，希望大家能自觉地应用.

　　7、作业：习题13.6A组1、2B组1、2

此文章共有2页  第 1 2 页