教学建议

　　1．知识结构：本小节主要学习正弦、余弦的概念，30°、45°、60°角的正弦、余弦值，一个锐角的正弦（余弦）值与它的余角的余弦（正弦）值之间的关系，以及应用上述知识解决一些简单问题（包括引言中的问题）等.

　　2．重点、难点分析

　　（1） 正弦、余弦函数的定义是本节的重点，因为它是全章乃至整个三角学的预备知识.有了正弦、余弦函数的定义，再学习正切和余切、解直角三角形、引入任意角三角函数便都有了基础.

　　（2） 正弦、余弦的概念隐含着角度与数值之间有一一对应关系的函数思想，并且用含有几个字母的符号组sinA，cosA来表示，学生过去未接触过，所以正弦、余弦的概念是难点.

　　3．理解一个锐角的正弦、余弦值的唯一性，是理解三角函数的核心.

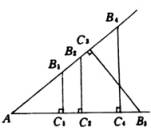
　　锐角的正弦、余弦值是这样规定的：当一个锐角确定了，那么这个锐角所在的直角三角形虽然有无穷多个，但它们都是彼此相似的.如上图，当 确定时，包含 的直角三角形有无穷多个，但它们彼此相似：

　　 ∽ ∽ ∽ ……因此，由于相似三角形的对应边成比例，所以这些三角形的对应边的比都是相等的.

　　这就是说，每当一个锐角确定了，包含这个角的直角三角形的上述2种比值也就唯一确定了，它们有确定不变的对应关系.为了简单地表达这些对应关系，我们引入了正（余）弦的说法，创造了sin 和cos这样的符号.

　　应当注意：单独写出三角函数的符号 或cos等是没有意义的.因为它们离开了确定的锐角是无法显示出它的含义；另一方面，这些符号和角写在一起时（如 ），它表示的就不再是角，而是一个特定的三角形的两条边的比值了（如 ）.真正理解并掌握这些，才真正掌握了这些符号的含义，才能正确地运用它们.

　　4． 我们应当学会认识任何位置的直角三角形中的一个锐角的正弦、余弦的表达式.

　　我们不仅应当熟练掌握如图那样的标准位置的直角三角形的正弦、余弦的表达式，而且能熟练地写出无论怎样放置的直角三角形的正弦、余弦的表达式.如， 如图所示，若 ，则有

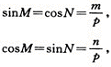
　　有的直角三角形隐藏在更复杂的图形中，我们也应能正确地写出所需要的三角函数表达式，如图中，ABCD是梯形， ，作 ， 我们应正确地写出如下的三角函数关系式：

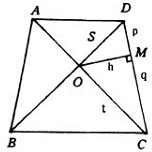
　　很显然，这些表达式提供给我们丰富的边与角间的数量关系.

　　5．特殊角的正弦、余弦值既容易导出，也便于记忆，应当熟悉掌握它们.

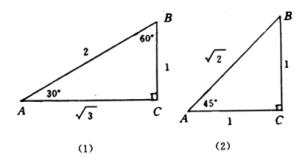
　　利用勾股定理，很容易求出含有 或 角的直角三角形三边的比；如图（1）和图（2）所示.

　　根据定义，有

　　另一方面，可以想像，当 时，边 与AC重合（即 ），所以

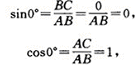
　　当 时，边AB与CB重合（即AB=CB），AC的长缩小为0，于是，有

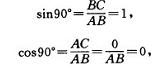
　　把以上结果可以集中列出下面的表：

　　6．教法建议：

　　（1）联系实际，提出问题

　　通过修建扬水站时，要沿斜坡铺设水管而提出要求水管最顶端离地面高度的问题，第一步把这问题归结于直角三角形中，第二步，再把这个问题归于直角三角形中，已知一个锐角和斜边的长，求这个锐角所对直角边的一个几何问题．同时指出在这种情况下，用已学过的勾股定理是解决不了的．激发学生的学习兴趣，调动学生探索新途径，迫切需要学习新知识的积极性．在这章的第一节课，应抓住这个具有教育性，富于启发性的有利开端，为引进本章的重要内容：锐角三角函数作了十分必要的准备．

　　(2) 动手度量、总结规律、给出定义以含 的三角板为例让学生对大小不同的三角板进行度量，并引导学生得出规律： ，再进一步对含 的三角板进行度量，在探索同样的内容时，要用到勾股定理，又类似地得到，所有的这种等腰直角三角形中，都会得到 ,这时，应当即给出 的正弦的定义及符号，即 ，再对照图形，分别用a、b、c表示 、 、 的对边，得出 及 ， 就这样非常简洁地得到锐角三角函数的第一个定义，应充分利用课本中这种简练的处理手段，使学生建立起锐角三角函数的概念.

　　(3)加强数形结合思想的教学

　　“解直角三角形”编在几何教材中，突出了它的几何特点，但这只是从知识的系统性方面讲的，使它与几何前后知识可关系更紧密，便于学生理解和掌握，并没有改变它形数结合的本质，因此教学中要充分利用这部分教材，帮助学生掌握用代数方法解决几何问题的方法，提高在几何问题中注意运用代数知识的能力．

此文章共有3页  第 1 2 3 页