1、知识目标：

　　（1）使学生理解轴对称的概念；

　　（2）了解轴对称的性质及其应用；

　　（3）知道轴对称图形与轴对称的区别.

　　2、能力目标：

　　（1）通过轴对称和轴对称图形的学习，提高学生的观察辨析图形的能力和画图能力；

　　（2）通过实际问题的练习，提高学生解决实际问题的能力.

　　3、情感目标：

　　（1）通过自主学习的发展体验获取数学知识的感受；

　　（2）通过轴对称图形的学习，体现数学中的美，感受数学中的美．

　　教学重点：轴对称和轴对称图形的概念，轴对称的性质及判定

　　教学难点：区分轴对称和轴对称图形的概念

　　教学用具：直尺，微机

　　教学方法：观察实验

　　教学过程：

　　1、概念：（阅读教材，回答问题）

　　（1）对称轴

　　（2）轴对称

　　（3）轴对称图形

　　学生动手实验，说明上述概念．最后总结轴对称及轴对称图形这两个概念的区别：

　　轴对称涉及两个图形，是两个图形的位置关系．轴对称图形只是针对一个图形而言．

　　轴对称和轴对称图形都有对称轴，如果把轴对称的两个图形看成一个整体，那么它就是一个轴对称图形；如果把轴对称图形沿对称轴分成两部分，那么这两个图形就关于这条直线对称．

　　2、定理的获得

　　（投影）：观察轴对称的两个图形是否为全等形

　　定理1：关于某条直线对称的两个图形是全等形

　　由此得出：

　　定理2：如果两个图形关于某直线对称，那么对称轴是对应点连线的垂直平分线．

　　启发学生，写出此定理的逆命题，并判断是否为真命题?由此得到：

　　逆定理：如果两个图形的对应点连线被同一条直线垂直平分，那么这两个图形关于这条直线对称．

　　学生继续观察得到

　　定理3：两个图形关于某直线对称，如果它们的对应线段或延长线相交，那么交点在对称轴上．

　　说明：上述定理2可以看成是轴对称图形的性质定理，逆定理则是判定定理．

　　上述问题的获得，都是由定理1引发、变换、延伸得到的．教师应充分抓住这次机会，培养学生变式问题的研究．

　　2、常见的轴对称图形

　　3、应用

　　例1　如图，已知：△ABC，直线MN，求作△A₁B₁C₁，使△A₁B₁C₁与△ABC关于MN对称．

　　分析：按照轴对称的概念，只要分别过A、B、C向直线MN作垂线，并将垂线段延长一倍即可得到点A、B、C关于直线MN的对称点，连结所得到的这三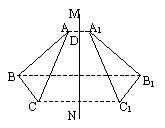个点．

　　作法：（1）作AD⊥MN于D，延长AD至A₁使A₁D＝AD，

　　得点A的对称点A₁

　　（2）同法作点B、C关于MN的对称点B_1、、C₁

　　（3）顺次连结A₁、B₁、C₁

　　∴△A₁B₁C₁即为所求

此文章共有2页  第 1 2 页