 打印本文
打印本文  关闭窗口
关闭窗口 有理数的乘方
一、素质教育目标
(一)知识教学点
1.理解有理数乘方的意义.
2.掌握有理数乘方的运算.
(二)能力训练点
1.培养学生观察、分析、比较、归纳、概括的能力.
2.渗透转化思想.
(三)德育渗透点:培养学生勤思、认真和勇于探索的精神.
(四)美育渗透点
把![]() 记成
记成![]() ,显示了乘方符号的简洁美.
,显示了乘方符号的简洁美.
二、学法引导
1.教学方法:引导探索法,尝试指导,充分体现学生主体地位.
2.学生学法:![]() 探索
探索![]() 的性质→练习巩固
的性质→练习巩固
三、重点、难点、疑点及解决办法
1.重点:有理数的乘方运算.
2.难点:有理数的乘方运算的符号法则.
3.疑点:①乘方和幂的区别.
②![]() 与
与![]() 的区别.
的区别.
四、课时安排
1课时
五、教具学具准备
投影仪、自制胶片.
六、师生互动活动设计
教师引导类比,学生讨论归纳乘方的概念,教师出示探索性练习,学生讨论归纳乘方的性质,教师出示巩固性练习,学生多种形式完成.
七、教学步骤
(一)创设情境,导入新课
师:在小学我们已经学过:![]() 记作
记作![]() ,读作
,读作![]() 的平方(或
的平方(或![]() 的二次方);
的二次方);![]() 记作
记作![]() ,读作
,读作![]() 的立方(或
的立方(或![]() 的三次方);那么
的三次方);那么![]() 可以记作什么?读作什么?
可以记作什么?读作什么?
生:可以记作![]() ,读作
,读作![]() 的四次方.
的四次方.
师:![]() 呢?
呢?
生:可以记作![]() ,读作
,读作![]() 的五次方.
的五次方.
师:![]() (
(![]() 为正整数)呢?
为正整数)呢?
生:可以记作![]() ,读作
,读作![]() 的
的![]() 次方.
次方.
师:很好!把![]() 个
个![]() 相乘,记作
相乘,记作![]() ,既简单又明确.
,既简单又明确.
【教法说明】教师给学生创设问题情境,鼓励学生积极参与,大大调动了学生学习的积极性.同时,使学生认识到数学的发展是不断进行推广的,![]() 是由计算正方形的面积得到的,
是由计算正方形的面积得到的,![]() 是由计算正方体和体积得到的,而
是由计算正方体和体积得到的,而![]() ,
,![]() ……
……![]() 是学生通过类推得到的.
是学生通过类推得到的.
师:在小学对底数![]() ,我们只能取正数.进入中学以后我们学习了有理数,那么
,我们只能取正数.进入中学以后我们学习了有理数,那么![]() 还可取哪些数呢?请举例说明.
还可取哪些数呢?请举例说明.
生:还可取负数和零.例如:0×0×0记![]() ,(-2)×(-2)×(-2)×(-2)记作
,(-2)×(-2)×(-2)×(-2)记作![]() .
.
非常好!对于![]() 中的
中的![]() ,不仅可以取正数,还可以取0和负数,也就是说
,不仅可以取正数,还可以取0和负数,也就是说![]() 可以取任意有理数,这就是我们今天研究的课题:有理数的乘方(板书).
可以取任意有理数,这就是我们今天研究的课题:有理数的乘方(板书).
【教法说明】对于![]() 的范围,是在教师的引导下,学生积极动脑参与,并且根据初一学生的认知水平,分层逐步说明
的范围,是在教师的引导下,学生积极动脑参与,并且根据初一学生的认知水平,分层逐步说明![]() 可以取正数,可以取零,可以取负数,最后总结出
可以取正数,可以取零,可以取负数,最后总结出![]() 可以取任意有理数.
可以取任意有理数.
(二)探索新知,讲授新课
1.求![]() 个相同因数的积的运算,叫做乘方.
个相同因数的积的运算,叫做乘方.
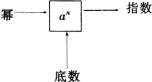
乘方的结果叫做幂,相同的因数叫做底数,相同的因数的个数叫做指数.一般地,在![]() 中,
中,![]() 取任意有理数,
取任意有理数,![]() 取正整数.
取正整数.
注意:乘方是一种运算,幂是乘方运算的结果.![]() 看作是
看作是![]() 的
的![]() 次方的结果时,也可读作
次方的结果时,也可读作![]() 的
的![]() 次幂.
次幂.
巩固练习(出示投影1)
(1)在![]() 中,底数是__________,指数是___________,
中,底数是__________,指数是___________,![]() 读作__________或读作___________;
读作__________或读作___________;
(2)在![]() 中,-2是__________,4是__________,
中,-2是__________,4是__________,![]() 读作__________或读作__________;
读作__________或读作__________;
(3)在![]() 中,底数是_________,指数是__________,
中,底数是_________,指数是__________,![]() 读作__________;
读作__________;
(4)5,底数是___________,指数是_____________.
【教法说明】此组练习是巩固乘方的有关概念,及时反馈学生掌握情况.(2)、(3)小题的区别![]() 表示底数是-2,指数是4的幂;而
表示底数是-2,指数是4的幂;而![]() 表示底数是2,指数是4的幂的相反数.为后面的计算做铺垫.通过第(4)小题指出一个数可以看作这个数本身的一次方,如5就是
表示底数是2,指数是4的幂的相反数.为后面的计算做铺垫.通过第(4)小题指出一个数可以看作这个数本身的一次方,如5就是![]() ,指数1通常省略不写.
,指数1通常省略不写.
师:到目前为止,对有理数业说,我们已经学过几种运算?分别是什么?其运算结果叫什么?
学生活动:同学们思考,前后桌同学互相讨论交流,然后举手回答.
生:到目前为止,已经学习过五种运算,它们是:
运算:加、减、乘、除、乘方;
运算结果:和、差、积、商、幂;
教师对学生的回答给予评价并鼓励.
【教法说明】注重学生在认知过程中的思维.主动参与,通过学生讨论、归纳得出的知识,比教师的单独讲解要记得牢,同时也培养学生归纳、总结的能力.
师:我们知道,乘方和加、减、乘、除一样,也是一种运算,如何进行乘方运算?请举例说明.
学生活动:学生积极思考,同桌相互讨论,并在练习本上举例.
【教法说明】通过学生积极动脑,主动参与,得出可以利用有理数的乘法运算来进行有理数乘方的运算.向学生渗透转化的思想.
2.练习:(出示投影2)
计算:1.(1)2, (2)![]() , (3)
, (3)![]() , (4)
, (4)![]() .
.
2.(1)![]() ,
,![]() ,
,![]() ,
,![]() .
.
(2)-2,![]() ,
,![]() .
.
3.(1)0, (2)![]() , (3)
, (3)![]() , (4)
, (4)![]() .
.
学生活动:学生独立完成解题过程,请三个学生板演,教师巡回指导,待学生完成后,师生共同评价对错,并予以鼓励.
师:请同学们观察、分析、比较这三组题中,每组题中底数、指数和幂之间有什么联系?
先让学生独立思考,教师边巡视边做适当提示.然后让学生讨论,老师加入某一小组.
生:正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数,零的任何次幂都是零.
师:请同学们继续观察![]() 与
与![]() ,
,![]() 与
与![]() 中,底数、指数和幂之间有何联系?你能得出什么结论呢?
中,底数、指数和幂之间有何联系?你能得出什么结论呢?
学生活动:学生积极思考,同桌之间、前后桌之间互相讨论.
生:互为相反数的两个数的奇次幂仍互为相反数,偶次幂相等.
师:请同学思考一个问题,任何一个数的偶次幂是什么数?
生:任何一个数的偶次幂是非负数.
师:你能把上述结论用数学符号表示吗?
生:(1)当![]() 时,
时,![]() (
(![]() 为正整数);
为正整数);
(2)当![]()
![]()
(3)当![]() 时,
时,![]() (
(![]() 为正整数);
为正整数);
(4)![]() (
(![]() 为正整数);
为正整数);
![]() (
(![]() 为正整数);
为正整数);
![]() (
(![]() 为正整数,
为正整数,![]() 为有理数).
为有理数).
【教法说明】教师把重点放在教学情境的设计上,通过学生自己探索,获取知识.教师要始终给学生创造发挥的机会,注重学生参与.学生通过特殊问题归纳出一般性的结论,既训练学生归纳总结的能力和口头表达的能力,又能使学生对法则记得牢,领会的深刻.
再做一组练习(出示投影3)
计算:(1)![]() ,
,![]() ,
,![]() ;
;
(2)![]() ,
,![]() ,
,![]() ;
;
(3)![]() ,
,![]() ,
,![]() .
.
学生活动:学生在练习本上独立完成后,同桌交换,互相纠正.然后,教师引导学生纵向观察(1)题和(2)题的形式和计算结果有什么区别?![]() 中底数是-3,而
中底数是-3,而![]() 题中,底数是3.因此
题中,底数是3.因此![]() ,
,![]() .可见,以负数作为底数时,这个负数必加括号,而不加括号的底数一定不是负数.
.可见,以负数作为底数时,这个负数必加括号,而不加括号的底数一定不是负数.
师:哪位同学能用乘方的一般式说明这个问题呢?
生:![]() 的底数是
的底数是![]() ,表示
,表示![]() 个
个![]() 相乘,
相乘,![]() 是
是![]() 的相反数,这就是
的相反数,这就是![]() 与
与![]() 的区别.
的区别.
师:引导学生观察(3)题,![]() 与
与![]() 两者从意义上截然不同:
两者从意义上截然不同:
![]() ,而
,而![]() .因此,要特别注意:当底数是分数时,这个分数一定要加括号,不加括号的底数不是分数.计算带分数的乘方一般应化为假分数.
.因此,要特别注意:当底数是分数时,这个分数一定要加括号,不加括号的底数不是分数.计算带分数的乘方一般应化为假分数.
【教法说明】同桌之间相互纠正,有时比师生之间的纠正效果会更好.通过学生实际计算、纠错,让他们自己体会到负数与分数的乘方要加括号.这样,学生自己获得的知识和方法,理解得更深刻,并能灵活运用.
(三)变式训练,培养能力
(出示投影4)
计算:
(1)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(2)![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(3)![]() ,
,![]() ,
,![]() ,
,![]() .
.
【教法说明】练习题的设计分层次,既注重基础知识,又注重了能力的培养,组织课内练习,获取学生掌握知识的反馈信息,对于学生存在的问题及时回授.
(四)课堂小结
师:今天我们一起学习了有理数的乘方.有理数的乘方运算可以利用有理数的乘法运算来进行.乘方与乘法有联系也有区别:联系是乘方本质是乘法,区别是乘方中积的因数要相同.为了更好地理解这一点,我们看下面的对比:
(出示投影5)
作乘法运算看 作乘方运算看
2×2×2=8 ![]()
因数是2 底数是2
因数的个数为3 指数是3
积是8 幂是8
【教法说明】小结揭示出乘方与乘法这两个知识点的联系,并找出它们之间的共同点和不同点,使学生将乘方知识与头脑中乘法的认识结构建立联系,从而形成新的知识体系.
(五)思考题
(出示投影6)
1.3的平方是多少?-3的平方是多少?平方得9的数有几个?有没有平方得-9的有理数?
2.已知![]() ,则
,则![]() .
.
3.计算![]() .
.
【教法说明】这组题目是让学有余力的学生应有所追求,进一步激发学生探索的热情,有利于发展他们的数学才能.2题是非负数和有理数乘方两知识点的综合应用,有助于培养学生分析问题和解决问题的能力.3题向学生渗透分类讨论的思想.
八、随堂练习
1.判断题
(1)![]() 中底数是
中底数是![]() ,指数是2( )
,指数是2( )
(2)一个有理数的平方总是大于0的( )
(3)![]() ( )
( )
(4)![]() ( )
( )
(5)![]() ( )
( )
(6)若![]() ,则
,则![]() ( )
( )
(7)当![]() 时,
时,![]() ( )
( )
(8)平方等于本身的数是0和1( )
2.填空题
(1)![]() 的意义是__________________,结果为________________;
的意义是__________________,结果为________________;
(2)![]() 的意义是__________________,结果为________________;
的意义是__________________,结果为________________;
(3)若![]() 且
且![]() ,则
,则![]() ;
;
(4)若![]() ,则
,则![]() ,
,![]() ,
,![]() ;
;
(5)平方小于10的整数有__________个,其和为___________,积为___________.
九、布置作业
课本第113页4、5.
十、板书设计
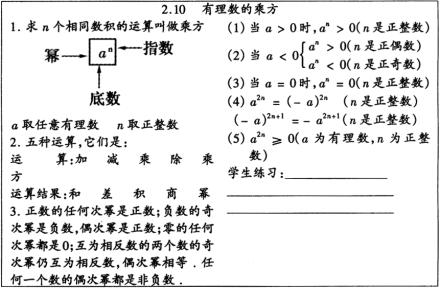
 打印本文
打印本文  关闭窗口
关闭窗口