1、教材分析

　　（1）知识结构

　　（2）重点、难点分析

　　重点：切线长定理及其应用．因切线长定理再次体现了圆的轴对称性，它为证明线段相等、角相等、弧相等、垂直关系等提供了理论依据，它属于工具知识，经常应用，因此它是本节的重点．

　　难点：与切线长定理有关的证明和计算问题．如120页练习题中第3题，它不仅应用切线长定理，还用到解方程组的知识，是代数与几何的综合题，学生往往不能很好的把知识连贯起来．

　　2、教法建议

　　本节内容需要一个课时．

　　（1）在教学中，组织学生自主观察、猜想、证明，并深刻剖析切线长定理的基本图形；对重要的结论及时总结；

　　（2）在教学中，以“观察——猜想——证明——剖析——应用——归纳”为主线，开展在教师组织下，以学生为主体，活动式教学．

教学目标

　　1．理解切线长的概念，掌握切线长定理；

　　2．通过对例题的分析，培养学生分析总结问题的习惯，提高学生综合运用知识解题的能力，培养数形结合的思想．

　　3．通过对定理的猜想和证明，激发学生的学习兴趣，调动学生的学习积极性，树立科学的学习态度．

　　教学重点:

　　切线长定理是教学重点

　　教学难点:

　　切线长定理的灵活运用是教学难点

　　教学过程设计:

　　（一）观察、猜想、证明，形成定理

　　 1、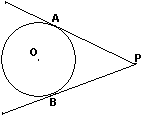切线长的概念．

　　如图，P是⊙O外一点，PA，PB是⊙O的两条切线，我们把线段PA，PB叫做点P到⊙O的切线长．

　　引导学生理解：切线和切线长是两个不同的概念，切线是直线，不能度量；切线长是线段的长，这条线段的两个端点分别是圆外一点和切点，可以度量.

　　2、观察

　　利用电脑变动点P 的位置，观察图形的特征和各量之间的关系．

　　3、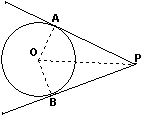猜想

　　引导学生直观判断，猜想图中PA是否等于PB． PA＝PB．

　　4、证明猜想，形成定理．

　　猜想是否正确。需要证明．

　　组织学生分析证明方法．关键是作出辅助线OA，OB，要证明PA＝PB．

　　想一想：根据图形，你还可以得到什么结论？

　　∠OPA＝∠OPB(如图)等．

　　切线长定理：从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角．

　　5、归纳：

　　把前面所学的切线的5条性质与切线长定理一起归纳切线的性质

　　6、切线长定理的基本图形研究

　　如图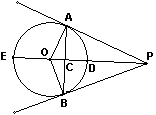，PA，PB是⊙O的两条切线，A，B为切点．直线OP交⊙O于点D，E，交AP于C

　　(1)写出图中所有的垂直关系；

　　(2)写出图中所有的全等三角形；

　　(3)写出图中所有的相似三角形；

　　(4)写出图中所有的等腰三角形．

　　说明：对基本图形的深刻研究和认识是在学习几何中关键，它是灵活应用知识的基础．

　　（二）应用、归纳、反思

　　例1、已知：如图，P为⊙O外一点，PA，PB为⊙O的切线，

　　A和B是切点，BC是直径．

　　求证：AC∥OP．

　　分析：从条件想，由P是⊙O外一点，PA、PB为⊙O的切线，A，B是切点可得PA＝PB，∠APO＝∠BPO，又由条件BC是直径，可得OB＝OC，由此联想到与直径有关的定理“垂径定理”和“直径所对的圆周角是直角”等．于是想到可能作辅助线AB.

　　从结论想，要证AC∥OP，如果连结AB交OP于O，转化为证CA⊥AB，OP ⊥AB，或从OD为△ABC的中位线来考虑．也可考虑通过平行线的判定定理来证，可获得多种证法．

　　证法一．如图．连结AB．

　　　PA，PB分别切⊙O于A，B

　　　∴PA＝PB∠APO＝∠BPO

　　　∴ OP ⊥AB

　　　又∵BC为⊙O直径

　　　∴AC⊥AB

　　　∴AC∥OP (学生板书)

　　证法二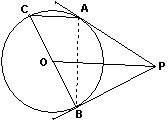．连结AB，交OP于D

　　　PA，PB分别切⊙O于A、B

　　　∴PA＝PB∠APO＝∠BPO  

　　　∴AD＝BD

　　　又∵BO=DO

　　　∴OD是△ABC的中位线

　　　∴AC∥OP

　　证法三．连结AB，设OP与AB弧交于点E

　　　PA，PB分别切⊙O于A、B

　　　∴PA＝PB

　　　∴ OP ⊥AB

　　　∴ =

　　　∴∠C＝∠POB

　　　∴AC∥OP

　　反思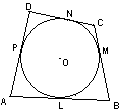：教师引导学生比较以上证法，激发学生的学习兴趣，培养学生灵活应用知识的能力．

此文章共有2页  第 1 2 页