圆周长、弧长(一)

　　教学目标：

　　1、初步掌握圆周长、弧长公式；

　　2、通过弧长公式的推导，培养学生探究新问题的能力；

　　3、调动学生的积极性，培养学生的钻研精神;

　　4、进一步培养学生从实际问题中抽象出数学模型的能力，综合运用所学知识分析问题和解决问题的能力．

　　教学重点：弧长公式．

　　教学难点：正确理解弧长公式．

　　教学活动设计：

　　（一）复习（圆周长）

　　已知⊙O半径为R，⊙O的周长C是多少？

C=2πR

　　这里π=3.14159…，这个无限不循环的小数叫做圆周率．

　　由于生产、生活实际中常遇到有关弧的长度计算，那么怎样求一段弧的长度呢？

　　提出新问题：已知⊙O半径为R，求n°圆心角所对弧长．

　　（二）探究新问题、归纳结论

　　教师组织学生探讨（因为问题并不难，学生完全可以自己研究得到公式）．

　　研究步骤：

　　（1）圆周长C=2πR；

　　（2）1°圆心角所对弧长= ；

　　（3）n°圆心角所对的弧长是1°圆心角所对的弧长的n倍；

　　（4）n°圆心角所对弧长= ．

　　归纳结论：若设⊙O半径为R， n°圆心角所对弧长l，则

  （弧长公式）

　　（三）理解公式、区分概念

　　教师引导学生理解：

　　（1）在应用弧长公式 进行计算时，要注意公式中n的意义．n表示1°圆心角的倍数，它是不带单位的；

　　（2）公式可以理解记忆（即按照上面推导过程记忆）；

　　（3）区分弧、弧的度数、弧长三概念．度数相等的弧，弧长不一定相等，弧长相等的弧也不一定是等孤，而只有在同圆或等圆中，才可能是等弧．

　　（四）初步应用

　　例1、已知：如图，圆环的外圆周长C₁=250cm，内圆周长C₂=150cm，求圆环的宽度d (精确到1mm)．

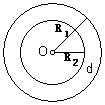　　 分析：（1）圆环的宽度与同心圆半径有什么关系？

　　（2）已知周长怎样求半径？

　　（学生独立完成）

　　解：设外圆的半径为R₁，内圆的半径为R₂，则

　　d= ．

　　∵ ， ，

　　∴ （cm）

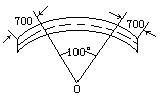　　 例2，弯制管道时，先按中心线计算展直长度，再下料，试计算图所示管道的展直长度L(单位：mm，精确到1mm)

　　教师引导学生把实际问题抽象成数学问题，渗透数学建模思想．

　　解：由弧长公式，得

　　 （mm）

　　所要求的展直长度

　　L （mm）

　　答：管道的展直长度为2970mm．

　　课堂练习：P176练习1、4题．

　　（五）总结

　　知识：圆周长、弧长公式；圆周率概念；

　　能力：探究问题的方法和能力，弧长公式的记忆方法；初步应用弧长公式解决问题．

　　（六）作业  教材P176练习2、3；P186习题3．

此文章共有2页  第 1 2 页