教学目标]

1．会阐述角平分线的性质定理及其逆定理。

2．会应用角平分线定理及其逆定理证明两条线段相等或两个角相等。

3．渗透点的集合的思想。

此外，教学中折纸、画图、文字──符号的翻译活动，有助于学生联想、探索、概括能力的培养。

[引导性材料]

用纸剪一个角，把纸片对折，使角的两边叠合在一起，再把纸片展开，你看到了什么？

把对折的纸片继续任意折一次，然后把纸片展开，又看到了什么？

[教学设计]

从上面折纸中我们发现，纸片第一次对折后的折痕是这个角的平分线；再折一次又会出现两条折痕，而且这两条折痕是等长的（如图3．9－1中的PM、PN）。由此，我们又可以发现，这种等长的折痕可以折去无数对，可是角的平分线除了有平分角的性质，还有其它的性质。

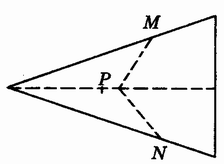
图3．9－1

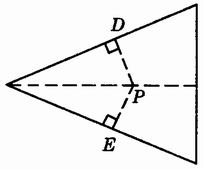
图3．9－2

操作：（l）折出如图3．9－2中的折痕PD、PE。

（2）你和同桌用三角扳检测你们所折的折痕是否符合图示的要求。

画一画：按照折纸的顺序画出一个角的如图3．9－2中的三条折痕，并度量所画PD、PE是否等长？

问题1：你能用文字语言阐述所画图形的性质吗？

说明：1．设计折纸和画一画的活动，实质是丰富学生对角平分线性质的感知，有利于学生能借助直观从而准确的用文字语言揭示角平分线的性质。

2．由于部分学生常常把“过角平分线上一点向角两边画垂线段”与“过角平分线上一点画角平分线垂线”混为一谈，因此设计操作（l）、（2），为学生能正确画出符合要求的图形，从直观上以及三角板的正确

使用上都作了恰当的铺垫，同时也为定理一的推证作准备。

问题2：根据命题“在角平分线上的点到这个角的两边的距离相等”，用符号语言填写下表：

（推证定理1）

问题3：根据下表中的图形和已知事项，猜想由已知事项可推出的事项，并用符号语言填写下表：

图形	已知事项	由已知事项推出的事项
	PD⊥OB，PE⊥OA，垂足为D、E，PD＝PE。

PD⊥OB，PE⊥OA，垂足为D、E，PD＝PE。　

问题4：用文字语言表述上表中的已知事项和由已知事项推出的事项。

（推证定理2）

问题5：在一个角的内部，除角平分线上的点外，是否有到角的两边距离相等的点？为什么？

在一个角的平分线上，是否有到角的两边距离不相等的点？为什么？

（阅读课本“由定理1、2可知……所有点的集合”）

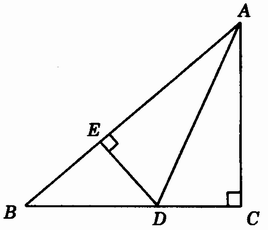
练一练：参照图3．9－3，填空：

　（1）∵AD平分∠BAC，

DC⊥AC，DE⊥AB（已知），

　∴DC＝DE（　）。

　（2）∵DC⊥AC，DE⊥AB，DC＝DE（已知），

∴点D在∠BAC的平分线上（　）。

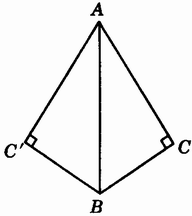
图3．9－3

[例题解析]

例：（补充例题）已知：如图3．9－4，∠C＝∠C′＝90°，AC＝AC′。

求证：（1）∠ABC＝∠ABC′；（2）BC＝BC′。（要求不用三角形全等判定）

证明：（1）∵∠C＝∠C′＝Rt∠(已知)

∴AC⊥BC，AC′⊥BC′（垂直的定义）。

又∵AC＝AC′（已知）

∴点A在∠CBC′的角平分线上（到一个角的两边的距离相等的点，在这个角的平分线）。

∴∠ABC＝∠ABC′

（2）∵∠C＝∠C′，∠ABC＝∠ABC′

　∴180°－（∠C＋∠ABC）＝180°－（∠C′＋∠ABC′）

（三角形内角和定理）。

　即∠BAC＝∠BAC′。

　∵BC⊥AC，BC′⊥AC′，

　∴BC＝BC′（在角平分线上的点到这个角的两边的距离相等）。

说明：通过三角形全等的判定的教学，多数学生能熟练地利用三角形全等论证几何命题，这对平面几何的学习有着一定的积极作用，但也会产生消极的作用。消极作用是使学生思考问题时偏向于某种模式，从而影响学生思维灵活性的发展，设计本例，并采用限制的措施，强迫学生打破思维定势，帮助学生克服思维定势的消极作用。

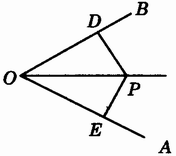
　图3．9－4

[课堂练习]

课本例题前练习

[小结]

角平分线的性质定理1、2题证明角相等、线段相等的新途径定理1常常用来证明线段相等（如例题（2））；定理2常常用来证明角相等或证明点在一个角的平分线上（如例题（l））。

[作业]

课本习题3．4第5、6、7题。