 打印本文
打印本文  关闭窗口
关闭窗口 一、教学目标
1.使学生理解并掌握分式的概念,了解有理式的概念;
2.使学生能够求出分式有意义的条件;
3.通过类比分数研究分式的教学,培养学生运用类比转化的思想方法解决问题的能力;
4.通过类比方法的教学,培养学生对事物之间是普遍联系又是变化发展的辨证观点的再认识.
二、重点、难点、疑点及解决办法
1.教学重点和难点 明确分式的分母不为零.
2.疑点及解决办法 通过类比分数的意义,加强对分式意义的理解.
三、教学过程
【新课引入】
前面所研究的因式分解问题是把整式分解成若干个因式的积的问题,但若有如下问题:某同学![]() 分钟做了60个仰卧起坐,每分钟做多少个?可表示为
分钟做了60个仰卧起坐,每分钟做多少个?可表示为![]() ,问,这是不是整式?请一位同学给它试命名,并说一说怎样想到的?(学生有过分数的经验,可猜想到分式)
,问,这是不是整式?请一位同学给它试命名,并说一说怎样想到的?(学生有过分数的经验,可猜想到分式)
【新课】
1.分式的定义
(1)由学生分组讨论分式的定义,对于“两个整式相除叫做分式”等错误,由学生举反例一一加以纠正,得到结论:
用![]() 、
、![]() 表示两个整式,
表示两个整式,![]() 就可以表示成
就可以表示成![]() 的形式.如果
的形式.如果![]() 中含有字母,式子
中含有字母,式子![]() 就叫做分式.其中
就叫做分式.其中![]() 叫做分式的分子,
叫做分式的分子,![]() 叫做分式的分母.
叫做分式的分母.
(2)由学生举几个分式的例子.
(3)学生小结分式的概念中应注意的问题.
①分母中含有字母.
②如同分数一样,分式的分母不能为零.
(4)问:何时分式的值为零?[以(2)中学生举出的分式为例进行讨论]
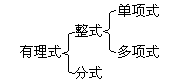
2.有理式的分类
请学生类比有理数的分类为有理式分类:
例1 当![]() 取何值时,下列分式有意义?
取何值时,下列分式有意义?
(1)![]() ;
;
解:由分母![]() 得
得![]() .
.
∴当![]() 时,原分式有意义.
时,原分式有意义.
(2)![]() ;
;
解:由分母![]() 得
得![]() .
.
∴当![]() 时,原分式有意义.
时,原分式有意义.
(3)![]() ;
;
解:∵![]() 恒成立,
恒成立,
∴![]() 取一切实数时,原分式都有意义.
取一切实数时,原分式都有意义.
(4)![]() .
.
解:由分母![]() 得
得![]() .
.
∴当![]() 且
且![]() 时,原分式有意义.
时,原分式有意义.
思考:若把题目要求改为:“当![]() 取何值时下列分式无意义?”该怎样做?
取何值时下列分式无意义?”该怎样做?
例2 当![]() 取何值时,下列分式的值为零?
取何值时,下列分式的值为零?
(1)![]() ;
;
解:由分子![]() 得
得![]() .
.
而当![]() 时,分母
时,分母![]() .
.
∴当![]() 时,原分式值为零.
时,原分式值为零.
小结:若使分式的值为零,需满足两个条件:①分子值等于零;②分母值不等于零.
(2)![]() ;
;
解:由分子![]() 得
得![]() .
.
而当![]() 时,分母
时,分母![]() ,分式无意义.
,分式无意义.
当![]() 时,分母
时,分母![]() .
.
∴当![]() 时,原分式值为零.
时,原分式值为零.
(3)![]() ;
;
解:由分子![]() 得
得![]() .
.
而当![]() 时,分母
时,分母![]() .
.
当![]() 时,分母
时,分母![]() .
.
∴当![]() 或
或![]() 时,原分式值都为零.
时,原分式值都为零.
(4)![]() .
.
解:由分子![]() 得
得![]() .
.
而当![]() 时,
时,![]() ,分式无意义.
,分式无意义.
∴没有使原分式的值为零的![]() 的值,即原分式值不可能为零.
的值,即原分式值不可能为零.
(四)总结、扩展
1.分式与分数的区别.
2.分式何时有意义?
3.分式何时值为零?
(五)随堂练习
1.填空题:
(1)当![]() 时,分式
时,分式![]() 的值为零
的值为零
(2)当![]() 时,分式
时,分式![]() 的值为零
的值为零
(3)当![]() 时,分式
时,分式![]() 的值为零
的值为零
2.教材P55中1、2、3.
八、布置作业
教材P56中A组3、4;B组(1)、(2)、(3).
九、板书设计
课题 例1
1.定义 例2
2.有理式分类
 打印本文
打印本文  关闭窗口
关闭窗口