一、知识结构

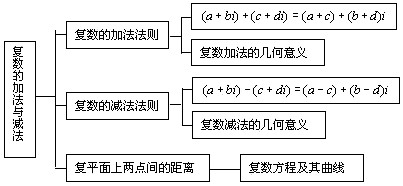
二、重点、难点分析

　　本节的重点是复数加法法则。难点是复数加减法的几何意义。复数加法法则是教材首先规定的法则，它是复数加减法运算的基础，对于这个规定的合理性，在教学过程中要加以重视。复数加减法的几何意义的难点在于复数加减法转化为向量加减法，以它为根据来解决某些平面图形的问题，学生对这一点不容易接受。

三、教学建议

　　（1）在复数的加法与减法中，重点是加法．教材首先规定了复数的加法法则．对于这个规定，应通过下面几个方面，使学生逐步理解这个规定的合理性：①当 时，与实数加法法则一致；②验证实数加法运算律在复数集中仍然成立；③符合向量加法的平行四边形法则．
　　（2）复数加法的向量运算讲解设 ，画出向量 ， 后，提问向量加法的平行四边形法则，并让学生自己画出和向量（即合向量） ，画出向量 后，问与它对应的复数是什么，即求点Z的坐标OR与RZ（证法如教材所示）．
　　（3）向学生介绍复数加法的三角形法则．讲过复数加法可按向量加法的平行四边形法则来进行后，可以指出向量加法还可按三角形法则来进行：如教材中图8－5（2）所示，求 与 的和，可以看作是求 与 的和．这时先画出第一个向量 ，再以 的终点为起点画出第二个向量 ，那么，由第一个向量起点O指向第二个向量终点Z的向量 ，就是这两个向量的和向量．
　　（4）向学生指出复数加法的三角形法则的好处．向学生介绍一下向量加法的三角形法则是有好处的：例如讲到当 与 在同一直线上时，求它们的和，用三角形法则来解释，可能比“画一个压扁的平行四边形”来解释容易理解一些；讲复数减法的几何意义时，用三角形法则也较平行四边形法则更为方便．
　　（5）讲解了教材例2后，应强调 （注意：这里 是起点， 是终点）就是同复数 － 对应的向量．点 ， 之间的距离 就是向量 的模，也就是复数 － 的模，即 ．

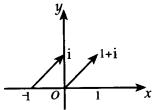　　例如，起点对应复数－1、终点对应复数 的那个向量（如图），可用 来表示．因而点 与 （ ）点间的距离就是复数     的模，它等于 。

 

教学设计示例

复数的减法及其几何意义

      教学目标

　　1．理解并掌握复数减法法则和它的几何意义．

　　2．渗透转化，数形结合等数学思想和方法，提高分析、解决问题能力．

　　3．培养学生良好思维品质（思维的严谨性，深刻性，灵活性等）．

教学重点和难点

　　重点：复数减法法则．

　　难点：对复数减法几何意义理解和应用．

教学过程设计

（一）引入新课

　　上节课我们学习了复数加法法则及其几何意义，今天我们研究的课题是复数减法及其几何意义．（板书课题：复数减法及其几何意义）

（二）复数减法

　　复数减法是加法逆运算，那么复数减法法则为（ + i）-（ + i）=（ - ）+（ - ）i，

1．复数减法法则

　　（1）规定：复数减法是加法逆运算；

　　（2）法则：（ + i）-（ + i）=（ - ）+（ - ）i（ ， ， ， ∈R）．

　　把（ + i）-（ + i）看成（ + i）+（-1）（ + i）如何推导这个法则．

（ + i）-（ + i）=（ + i）+（-1）（ + i）=（ + i）+（- - i）=（ - ）+（ - ）i．

　　推导的想法和依据把减法运算转化为加法运算．

　　推导：设（ + i）-（ + i）= + i（ ， ∈R）．即复数 + i为复数 + i减去复数 + i的差．由规定，得（ + i）+（ + i）= + i，依据加法法则，得（ + ）+（ + ）i= + i，依据复数相等定义，得

　　故（ + i）-（ + i）=（ - ）+（ - ）i．这样推导每一步都有合理依据．

　　我们得到了复数减法法则，两个复数的差仍是复数．是唯一确定的复数．

　　复数的加（减）法与多项式加（减）法是类似的．就是把复数的实部与实部，虚部与虚部分别相加（减），即（ + i）±（ + i）=（ ± ）+（ ± ）i．

（三）复数减法几何意义

　　我们有了做复数减法的依据——复数减法法则，那么复数减法的几何意义是什么？
　　设z= + i（ ， ∈R），z₁= + i（ ， ∈R），对应向量分别为 ， 如图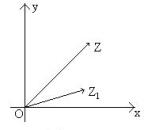

　　由于复数减法是加法的逆运算，设z=（ - ）+（ - ）i，所以z-z₁=z₂，z₂+z₁=z，由复数加法几何意义，以 为一条对角线， ₁为一条边画平行四边形，那么这个平行四边形的另一边 ₂所表示的向量OZ₂就与复数z-z₁的差（ - ）+（ - ）i对应，如图．

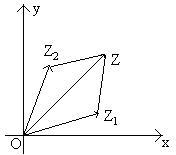
　　在这个平行四边形中与z-z₁差对应的向量是只有向量 ₂吗？ 

　　还有 ． 因为OZ₂ Z₁Z，所以向量 ，也与z-z₁差对应．向量 是以Z₁为起点，Z为终点的向量．

　　能概括一下复数减法几何意义是：两个复数的差z-z₁与连接这两个向量终点并指向被减数的向量对应．

（四）应用举例





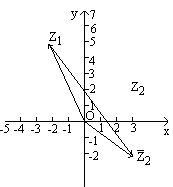
　　在直角坐标系中标Z₁（-2，5），连接OZ₁，向量 ₁与多数z₁对应，标点Z₂（3，2），Z₂关于x轴对称点Z₂（3，-2），向量 ₂与复数对应，连接，向量与的差对应（如图）．

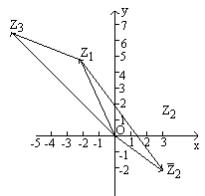
　　例2　根据复数的几何意义及向量表示，求复平面内两点间的距离公式．

　　解：设复平面内的任意两点Z₁，Z₂分别表示复数z₁，z₂，那么Z₁Z₂就是复数对应的向量，点之间的距离就是向量的模，即复数z₂-z₁的模．如果用d表示点Z₁，Z₂之间的距离，那么d=|z₂-z₁|．

　　例3  在复平面内，满足下列复数形式方程的动点Z的轨迹是什么．

　　（1）|z-1-i|=|z+2+i|；

　　方程左式可以看成|z-（1+i）|，是复数Z与复数1+i差的模．

　　几何意义是是动点Z与定点（1，1）间的距离．方程右式也可以写成|z-（-2-i）|，是复数z与复数-2-i差的模，也就是动点Z与定点（-2，-1）间距离．这个方程表示的是到两点（+1，1），（-2，-1）距离相等的点的轨迹方程，这个动点轨迹是以点（+1，1），（-2，-1）为端点的线段的垂直平分线．

　　（2）|z+i|+|z-i|=4；

　　方程可以看成|z-（-i）|+|z-i|=4，表示的是到两个定点（0，-1）和（0，1）距离和等于4的动点轨迹．满足方程的动点轨迹是椭圆．

　　（3）|z+2|-|z-2|=1．

　　这个方程可以写成|z-（-2）|-|z-2|=1，所以表示到两个定点（-2，0），（2，0）距离差等于1的点的轨迹，这个轨迹是双曲线．是双曲线右支．

　　由z₁-z₂几何意义，将z₁-z₂取模得到复平面内两点间距离公式d=|z1-z2|，由此得到线段垂直平分线，椭圆、双曲线等复数方程．使有些曲线方程形式变得更为简捷．且反映曲线的本质特征．

　　例4  设动点Z与复数z= + i对应，定点P与复数p= + i对应．求

　　（1）复平面内圆的方程；

　　解：设定点P为圆心，r为半径，如图

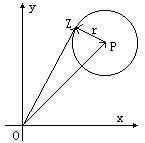
　　由圆的定义，得复平面内圆的方程|z-p|=r．

　　（2）复平面内满足不等式|z-p|＜r（r∈R₊）的点Z的集合是什么图形？

　　解：复平面内满足不等式|z-p|＜r（r∈R₊）的点的集合是以P为圆心，r为半径的圆面部分（不包括周界）．利用复平面内两点间距离公式，可以用复数解决解析几何中某些曲线方程．不等式等问题．

（五）小结

　　我们通过推导得到复数减法法则，并进一步得到了复数减法几何意义，应用复数减法几何意义和复平面内两点间距离公式，可以用复数研究解析几何问题，不等式以及最值问题．

（六）布置作业P193习题二十七：2，3，8，9．

 

探究活动