第二课时

教学目标

　　1．理解同向不等式，异向不等式概念；
　　2．掌握并会证明定理1，2，3；
　　3．理解定理3的推论是同向不等式相加法则的依据，定理3是移项法则的依据；
　　4．初步理解证明不等式的逻辑推理方法.

教学重点：定理1，2，3的证明的证明思路和推导过程

教学难点：理解证明不等式的逻辑推理方法

教学方法：引导式

教学过程

一、复习回顾

　　上一节课,我们一起学习了比较两实数大小的方法,主要根据的是实数运算的符号法则,而这也是推证不等式性质的主要依据,因此，我们来作一下回顾：

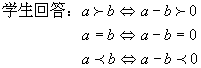
　　这一节课，我们将利用比较实数的方法， 来推证不等式的性质.

二、讲授新课

　　在证明不等式的性质之前,我们先明确一下同向不等式与异向不等式的概念.

　　1．同向不等式：两个不等号方向相同的不等式，例如： 是同向不等式.

　　　异向不等式：两个不等号方向相反的不等式.例如： 是异向不等式.

　　2．不等式的性质：

定理1：若 ，则

定理1说明，把不等式的左边和右边交换，所得不等式与原不等式异向.在证明时，既要证明充分性，也要证明必要性.

证明：∵ ，

∴

由正数的相反数是负数，得

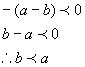
说明：定理1的后半部分可引导学生仿照前半部分推证，注意向学生强调实数运算的符号法则的应用.

定理2：若 ，且 ，则 .

证明：∵

∴

根据两个正数的和仍是正数，得

∴ 说明：此定理证明的主要依据是实数运算的符号法则及两正数之和仍是正数.

定理3：若 ，则

定理3说明，不等式的两边都加上同一个实数，所得不等式与原不等式同向.

证明：∵

          ∴

说明：（1）定理3的证明相当于比较 与 的大小，采用的是求差比较法；

（2）不等式中任何一项改变符号后，可以把它从一边移到另一边，理由是：根据定理3可得出：若 ，则 即 .

    定理3推论：若 .

证明:∵ ,

∴      ①

∵

∴       ②

由①、②得

说明：（1）推论的证明连续两次运用定理3然后由定理2证出；

　　（2）这一推论可以推广到任意有限个同向不等式两边分别相加，即：两个或者更多个同向不等式两边分别相加，所得不等式与原不等式同向；

　　（3）两个同向不等式的两边分别相减时，就不能作出一般的结论；

　　（4）定理3的逆命题也成立.（可让学生自证）

三、课堂练习

　　1．证明定理1后半部分；

　　2．证明定理3的逆定理.

说明：本节主要目的是掌握定理1，2，3的证明思路与推证过程，练习穿插在定理的证明过程中进行.

课堂小结

　　通过本节学习，要求大家熟悉定理1，2，3的证明思路，并掌握其推导过程，初步理解证明不等式的逻辑推理方法.

课后作业

　　1．求证：若

　　2．证明：若

板书设计

§6.1.2  不等式的性质

　1．同向不等式          3.定理2     4.定理3      5.定理3

　　异向不等式          　　证明          证明         推论

   2．定理1 证明          　 说明          说明         证明

第三课时

教学目标

　　1．熟练掌握定理1，2，3的应用；
　　2．掌握并会证明定理4及其推论1，2；
　　3．掌握反证法证明定理5.

教学重点：定理4，5的证明.

教学难点：定理4的应用.

教学方法：引导式

教学过程：

一、复习回顾

　　上一节课，我们一起学习了不等式的三个性质，即定理1，2，3，并初步认识了证明不等式的逻辑推理方法，首先，让我们来回顾一下三个定理的基本内容.

（学生回答）

　　好，我们这一节课将继续推论定理4、5及其推论，并进一步熟悉不等式性质的应用.

二、讲授新课

　　定理4：若

       　　　若

　　证明：

　　根据同号相乘得正，异号相乘得负，得

　　当

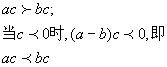
说明：（1）证明过程中的关键步骤是根据“同号相乘得正，异号相乘得负”来完成的；

　　　（2）定理4证明在一个不等式两端乘以同一个正数，不等号方向不变；乘以同一个负数，不等号方向改变.

推论1：若

　　证明：

　　      ①

　　又

　　∴     ②

　　由①、②可得 .

　　说明：（1）上述证明是两次运用定理4，再用定理2证出的；

　　　　　（2）所有的字母都表示正数，如果仅有 ，就推不出 的结论.

　　　　　（3）这一推论可以推广到任意有限个两边都是正数的同向不等式两边分别相乘.这就是说，两个或者更多个两边都是正数的同向不等式两边分别相乘，所得不等式与原不等式同向.

　　推论2：若

　　说明：（1）推论2是推论1的特殊情形；

　　　　　（2）应强调学生注意n∈N 的条件.

　　定理5：若

　　我们用反证法来证明定理5，因为反面有两种情形，即 ，所以不能仅仅否定了 ，就“归谬”了事，而必须进行“穷举”.

　　说明：假定 不大于 ，这有两种情况：或者 ，或者 .

　　由推论2和定理1，当 时，有 ；

　　当 时，显然有

　　这些都同已知条件 矛盾

　　所以 .

　　接下来，我们通过具体的例题来熟悉不等式性质的应用.

例2    已知

　　证明：由

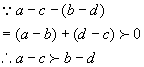
例3  已知

　　证明：∵

　　两边同乘以正数

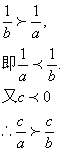
　　说明：通过例3，例4的学习，使学生初步接触不等式的证明，为以后学习不等式的证明打下基础.在应用定理4时，应注意题目条件，即在一个等式两端乘以同一个数时，其正负将影响结论.接下来，我们通过练习来进一步熟悉不等式性质的应用.

三、课堂练习

　　课本P₇练习1，2，3.

课堂小结

　　通过本节学习，大家要掌握不等式性质的应用及反证法证明思路，为以后不等式的证明打下一定的基础.

课后作业

　　课本习题6.1 4，5.

板书设计

§6.1.3  不等式的性质

定理4      推论1         定理5          例3     学生

内容                     内容        

证明        推论2         证明          例4       练习