 打印本文
打印本文  关闭窗口
关闭窗口 线性规划教学设计方案(二)
教学目标
巩固二元一次不等式和二元一次不等式组所表示的平面区域,能用此来求目标函数的最值.
重点难点
理解二元一次不等式表示平面区域是教学重点.
如何扰实际问题转化为线性规划问题,并给出解答是教学难点.
教学步骤
【新课引入】
我们知道,二元一次不等式和二元一次不等式组都表示平面区域,在这里开始,教学又翻开了新的一页,在今后的学习中,我们可以逐步看到它的运用.
【线性规划】
先讨论下面的问题
设 ![]() ,式中变量x、y满足下列条件
,式中变量x、y满足下列条件
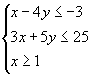 ①
①
求z的最大值和最小值.
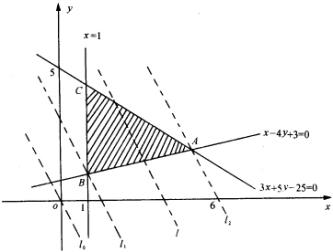
我们先画出不等式组①表示的平面区域,如图中 ![]() 内部且包括边界.点(0,0)不在这个三角形区域内,当
内部且包括边界.点(0,0)不在这个三角形区域内,当 ![]() 时,
时, ![]() ,点(0,0)在直线
,点(0,0)在直线 ![]() 上.
上.
作一组和 ![]() 平等的直线
平等的直线
![]()
可知,当l在 ![]() 的右上方时,直线l上的点
的右上方时,直线l上的点 ![]() 满足
满足 ![]() .
.
即 ![]() ,而且l往右平移时,t随之增大,在经过不等式组①表示的三角形区域内的点且平行于l的直线中,以经过点A(5,2)的直线l,所对应的t最大,以经过点
,而且l往右平移时,t随之增大,在经过不等式组①表示的三角形区域内的点且平行于l的直线中,以经过点A(5,2)的直线l,所对应的t最大,以经过点 ![]() 的直线
的直线 ![]() ,所对应的t最小,所以
,所对应的t最小,所以
![]()
在上述问题中,不等式组①是一组对变量x、y的约束条件,这组约束条件都是关于x、y的一次不等式,所以又称线性约束条件.
![]() 是欲达到最大值或最小值所涉及的变量x、y的解析式,叫做目标函数,由于
是欲达到最大值或最小值所涉及的变量x、y的解析式,叫做目标函数,由于 ![]() 又是x、y的解析式,所以又叫线性目标函数,上述问题就是求线性目标函数
又是x、y的解析式,所以又叫线性目标函数,上述问题就是求线性目标函数 ![]() 在线性约束条件①下的最大值和最小值问题.
在线性约束条件①下的最大值和最小值问题.
线性约束条件除了用一次不等式表示外,有时也有一次方程表示.
一般地,求线性目标函数在线性约束条件下的最大值或最小值的问题,统称为线性规划问题,满足线性约束条件的解 ![]() 叫做可行解,由所有可行解组成的集合叫做可行域,在上述问题中,可行域就是阴影部分表示的三角形区域,其中可行解(5,2)和(1,1)分别使目标函数取得最大值和最小值,它们都叫做这个问题的最优解.
叫做可行解,由所有可行解组成的集合叫做可行域,在上述问题中,可行域就是阴影部分表示的三角形区域,其中可行解(5,2)和(1,1)分别使目标函数取得最大值和最小值,它们都叫做这个问题的最优解.
【应用举例】
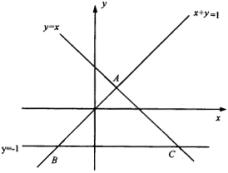 例1 解下列线性规划问题:求
例1 解下列线性规划问题:求 ![]() 的最大值和最小值,使式中的x、y满足约束条件
的最大值和最小值,使式中的x、y满足约束条件 
解:先作出可行域,见图中 ![]() 表示的区域,且求得
表示的区域,且求得 ![]() .
.
作出直线 ![]() ,再将直线
,再将直线 ![]() 平移,当
平移,当 ![]() 的平行线
的平行线 ![]() 过B点时,可使
过B点时,可使 ![]() 达到最小值,当
达到最小值,当 ![]() 的平行线
的平行线 ![]() 过C点时,可使
过C点时,可使 ![]() 达到最大值.
达到最大值.
![]()
通过这个例子讲清楚线性规划的步骤,即:
第一步:在平面直角坐标系中作出可行域;
第二步:在可行域内找出最优解所对应的点;
第三步:解方程的最优解,从而求出目标函数的最大值或最小值.
例2 解线性规划问题:求 ![]() 的最大值,使式中的x、y满足约束条件.
的最大值,使式中的x、y满足约束条件.
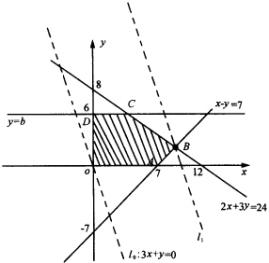
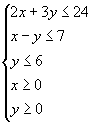
解:作出可行域,见图,五边形OABCD表示的平面区域.
作出直线 ![]() 将它平移至点B,显然,点B的坐标是可行域中的最优解,它使
将它平移至点B,显然,点B的坐标是可行域中的最优解,它使 ![]() 达到最大值,解方程组
达到最大值,解方程组 ![]() 得点B的坐标为(9,2).
得点B的坐标为(9,2).
∴ ![]()
这个例题可在教师的指导下,由学生解出.在此例中,若目标函数设为 ![]() ,约束条件不变,则z的最大值在点C(3,6)处取得.事实上,可行域内最优解对应的点在何处,与目标函数
,约束条件不变,则z的最大值在点C(3,6)处取得.事实上,可行域内最优解对应的点在何处,与目标函数 ![]() 所确定的直线
所确定的直线 ![]() 的斜率
的斜率 ![]() 有关.就这个例子而言,当
有关.就这个例子而言,当 ![]() 的斜率为负数时,即
的斜率为负数时,即 ![]() 时,若
时,若 ![]() (直线
(直线 ![]() 的斜率)时,线段BC上所有点都是使z取得最大值(如本例);当
的斜率)时,线段BC上所有点都是使z取得最大值(如本例);当 ![]() 时,点C处使z取得最大值(比如:
时,点C处使z取得最大值(比如: ![]() 时),若
时),若 ![]() ,可请同学思考.
,可请同学思考.
随堂练习
1.求 ![]() 的最小值,使式中的
的最小值,使式中的 ![]() 满足约束条件
满足约束条件
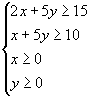
2.求 ![]() 的最大值,使式中
的最大值,使式中 ![]() 满足约束条件
满足约束条件
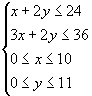
答案:1. ![]() 时,
时, ![]() .
.
2. ![]() 时,
时, ![]() .
.
总结提炼
1.线性规划的概念.
2.线性规划的问题解法.
布置作业
1.求 ![]() 的最大值,使式中的
的最大值,使式中的 ![]() 满足条件
满足条件
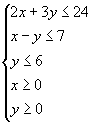
2.求 ![]() 的最小值,使
的最小值,使 ![]() 满足下列条件
满足下列条件
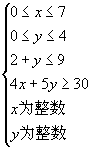
答案:1. ![]()
2.在可行域内整点中,点(5,2)使z最小, ![]()
探究活动
利润的线性规划
[分析]首先应考虑在平面直角坐标系中如何描述题中信息:“1997年的利润为5万元,1998年的利润为7万元,1999年的利润为8万元”,在确定这三点坐标后,如何运用这三点坐标,是仅用其中的两点,还是三点信息的综合运用,运用时要注意有其合理性、思考的方向可以考虑将通过特殊点的直线、平行某个线段的直线、与某些点距离最小的直线作为预测直线等等.
建立平面直角坐标系,设1997年的利润为5万元对应的点为 ![]() (0,5),1998年的利润为 7万元及1999年的利润为 8万元分别对应点
(0,5),1998年的利润为 7万元及1999年的利润为 8万元分别对应点 ![]() (1,7)和
(1,7)和 ![]() (2,8),那么
(2,8),那么
①若将过 ![]() 两点的直线作为预测直线
两点的直线作为预测直线 ![]() ,其方程为:
,其方程为: ![]() ,这样预测2001年的利润为13万元.
,这样预测2001年的利润为13万元.
②若将过 ![]() 两点的直线作为预测直线
两点的直线作为预测直线 ![]() ,其方程为:
,其方程为: ![]() ,这样预测2001年的利润为11万元.
,这样预测2001年的利润为11万元.
③若将过 ![]() 两点的直线作为预测直线
两点的直线作为预测直线 ![]() ,其方程为:
,其方程为: ![]() ,这样预测2001年的利润为10万元.
,这样预测2001年的利润为10万元.
④若将过 ![]() 及线段
及线段 ![]() 的中点
的中点 ![]() 的直线作为预测直线
的直线作为预测直线 ![]() ,其方程为:
,其方程为: ![]() ,这样预测2001年的利润为11.667万元.
,这样预测2001年的利润为11.667万元.
⑤若将过 ![]() 及
及 ![]() 的重心
的重心 ![]() (注:
(注: ![]() 为3年的年平均利润)的直线作为预测直线
为3年的年平均利润)的直线作为预测直线 ![]() ,其方程为:
,其方程为: ![]() ,这样预测2001年的利润为11.667万元.
,这样预测2001年的利润为11.667万元.
⑥若将过 ![]() 及
及 ![]() 的重心
的重心 ![]() 的直线作为预测直线
的直线作为预测直线 ![]() ,其方程为:
,其方程为: ![]() ,这样预测2001年的利润为10.667万元.
,这样预测2001年的利润为10.667万元.
⑦若将过 ![]() 且以线段
且以线段 ![]() 的斜率
的斜率 ![]() 为斜率的直线作为预测直线,则预测直线
为斜率的直线作为预测直线,则预测直线 ![]() 的方程为:
的方程为: ![]() ,这样预测2001年的利润为9万元.
,这样预测2001年的利润为9万元.
⑧若将过 ![]() 且以线段
且以线段 ![]() 的斜率
的斜率 ![]() 为斜率的直线作为预测直线,则预测直线
为斜率的直线作为预测直线,则预测直线 ![]() 的方程为:
的方程为: ![]() ,这样预测2001年的利润为11.5万元.
,这样预测2001年的利润为11.5万元.
⑨若将过点 ![]() 且以线段
且以线段 ![]() 的斜率
的斜率 ![]() 为斜率的直线,作为预测直线,则预测直线
为斜率的直线,作为预测直线,则预测直线 ![]() 的方程为;
的方程为; ![]() ,这样预测2001年的利润为12万元.
,这样预测2001年的利润为12万元.
⑩若将过 ![]() 且以线段
且以线段 ![]() 的斜率
的斜率 ![]() 与线段
与线段 ![]() 的斜率
的斜率 ![]() 的平均数为斜率的直线作为预测直线,则预测直线
的平均数为斜率的直线作为预测直线,则预测直线 ![]() 的方程为:
的方程为: ![]() ,这样预测2001年的利润为12万元.
,这样预测2001年的利润为12万元.
如此这样,还有其他方案,在此不—一列举.
[思考](1)第⑤种方案与第④种方案的结果完全一致,这是为什么?
(2)第⑦种方案中, ![]() 的现实意义是什么?
的现实意义是什么?
(3)根据以上的基本解题思路,请你思考新的方案.如方案⑥中,过 ![]() 的重心
的重心 ![]() ,找出以
,找出以 ![]() 为斜率的直线中与
为斜率的直线中与 ![]() 两点的距离的平方和最小的直线作为预测直线.
两点的距离的平方和最小的直线作为预测直线.
(4)根据以上结论及你自己的答案估计一下利润的范围,你预测的利润频率出现最多的是哪一个值?你认为将你预测的结论作怎样的处理,使之得到的利润预测更为有效?如果不要求用线性预测,你能得出什么结果?
 打印本文
打印本文  关闭窗口
关闭窗口