 打印本文
打印本文  关闭窗口
关闭窗口 教学目标
(1)了解线性规化的意义以及线性约束条件、线性目标函数、线性规化问题、可行解、可行域以及最优解等基本概念;
(2)了解线性规化问题的图解法;
(3)培养学生搜集、分析和整理信息的能力,在活动中学会沟通与合作,培养探索研究的能力和所学知识解决实际问题的能力;
(4)引发学生学习和使用数学知识的兴趣,发展创新精神,培养实事求是、理论与实际相结合的科学态度和科学道德.
教学建议
一、重点难点分析
学以致用,培养学生“用数学”的意识是本节的重要目的。学习线性规划的有关知识其最终目的就是运用它们去解决一些生产、生活中问题,因而本节的教学重点是:线性规划在实际生活中的应用。困难大多是如何把实际问题转化为数学问题(既数学建模),所以把一些生产、生活中的实际问题转化为线性规划问题,就是本节课的教学难点。突破这个难点的关键就在于尽快熟悉生活,了解实际情况,并与所学知识紧密结合起来。
二、教法建议
(l)建议可适当采用电脑多媒体和投影仪等先进手段来辅助教学,以增加课堂容量,增强直观性,进而提高课堂效率.
(2)课堂上可以设计几个实际让学生分组研讨解答,一方面是复习线性规划问题的一般解法,为总结线性规划问题的数学模型和常见类型作铺垫;另一方面,也为接下来到外面分组调研积累经验,让学生在讨论、探究过程中初步学会沟通与合作,共同完成活动任务.
(3)确定研究课题,建议各小组以三个常见问题为主,或者根据本小组实际自拟课题.
(4)活动安排,建议要求各小组分式明确,团结协作,听从指挥,注意安全.学生研究活动的成果,可以用研究报告或论文的形式体现.一切以学生自己的自主探究活动为主,教师不能越俎代庖.
(5)对学生在课余时间开展的研究性课题,建议作做好成果展示、评估和交流.展示不仅可以让全体学生来分享成果,享受成功的喜悦,而且还可以锻炼学生的组织表达能力,增强学生的自信心.通过评估,可以使同学清楚地看到自己的优点与不足.通过交流研讨,分享成果,进行思维碰撞,使认识和情感得到提升.
教学设计方案
教学目标
(1)了解线性规划的意义以及线性约束条件、线性目标函数、线性规化问题、可行解、可行域以及最优解等基本概念;
(2)了解线性规划问题的图解法,并能应用它解决一些简单的实际问题;
(3)培养学生观察、联想以及作图的能力,渗透集合、化归、数形结合的数学思想,提高学生“建模”和解决实际问题的能力;
(4)结合教学内容,培养学生学习数学的兴趣和“用数学”的意识,激励学生勇于创新.
重点难点
理解二元一次不等式表示平面区域是教学重点。
如何扰实际问题转化为线性规划问题,并给出解答是教学难点。
教学步骤
(一)引入新课
我们已研究过以二元一次不等式组为约束条件的二元线性目标函数的线性规划问题。那么是否有多个两个变量的线性规划问题呢?又什么样的问题不用线性规划知识来解决呢?
(二)线性规划问题的教学模型
线性规划研究的是线性目标函数在线性约束条件下取最大值或最小值问题,一般地,线性规划问题的数字模型是
已知 其中
其中 ![]() 都是常数,
都是常数, ![]() 是非负变量,求
是非负变量,求![]() 的最大值或最小值,这里
的最大值或最小值,这里 ![]() 是常量。
是常量。
前面我们计论了两个变量的线性规划问题,这类问题可以用图解法来求最优解,涉及更多变量的线性规划问题不能用图解法求解。比如线性不等式 ![]() 不能用图形来表示它,那么对四元线性规划问题就不能用图形来求解了,对这样的线性规划问题怎样求解,同学们今后在大学学习中会得到解决。
不能用图形来表示它,那么对四元线性规划问题就不能用图形来求解了,对这样的线性规划问题怎样求解,同学们今后在大学学习中会得到解决。
线性规划在实际中的应用
线性规划的理论和方法主要在两类问题中得到应用,一是在人力、物力、资金等资源一定的条件下,如何使用它们来完成最多的任务;二是给定一项任务,如何合理安排和规划,能以最少的人力、物力、资金等资源来完成该项任务,常见问题有:
1.物调运问题
例如,已知 ![]() 两煤矿每年的产量,煤需经
两煤矿每年的产量,煤需经 ![]() 两个车站运往外地,
两个车站运往外地, ![]() 两个车站的运输能力是有限的,且已知
两个车站的运输能力是有限的,且已知 ![]() 两煤矿运往
两煤矿运往 ![]() 两个车站的运输价格,煤矿应怎样编制调运方案,能使总运费最小?
两个车站的运输价格,煤矿应怎样编制调运方案,能使总运费最小?
2.产品安排问题
例如,某工厂生产甲、乙两种产品,每生产一个单位的甲种或乙种产品需要的A、B、C三种材料的数量,此厂每月所能提供的三种材料的限额都是已知的,这个工厂在每个月中应如何安排这两种产品的生产,能使每月获得的总利润最大?
3.下料问题
例如,要把一批长钢管截成两种规格的钢管,应怎样下料能使损耗最小?
4.研究一个例子
下面的问题,能否用线性规划求解?如能,请同学们解出来。
某家具厂有方木料 ![]() ,五合板
,五合板 ![]() ,准备加工成书桌和书橱出售,已知生产每张书桌需要方木料
,准备加工成书桌和书橱出售,已知生产每张书桌需要方木料 ![]() 、五合板
、五合板 ![]() ,生产每个书橱需要方木料
,生产每个书橱需要方木料 ![]() 、五合板
、五合板 ![]() ,出售一张书桌可获利润80元,出售一个书橱可获利润120元,如果只安排生产书桌,可获利润多少?如何只安排生产书橱,可获利润多少?怎样安排生产时可使所得利润最大?
,出售一张书桌可获利润80元,出售一个书橱可获利润120元,如果只安排生产书桌,可获利润多少?如何只安排生产书橱,可获利润多少?怎样安排生产时可使所得利润最大?
A.教师指导同学们逐步解答:
(1)先将已知数据列成下表
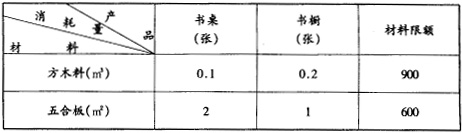
(2)设生产书桌x张,生产书橱y张,获利润为z元。
分析:显然这是一个二元线性问题,可归结于线性规划问题,并可用图解法求解。
(3)目标函数 ![]()
①在第一个问题中,即只生产书桌,则![]() ,约束条件为
,约束条件为
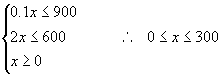
∴ 最多生产300张书桌,获利润 ![]() 元
元
这样安排生产,五合板先用光,方木料只用了 ![]() ,还有
,还有 ![]() 没派上用场。
没派上用场。
②在第二个问题中,即只生产书橱,则![]() ,约束条件是
,约束条件是
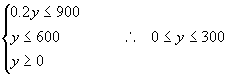
∴ 最多生产600张书橱,获利润 ![]() 元
元
这样安排生产,五合板也全用光,方木料用去了 ![]() ,仍有
,仍有 ![]() 没派上用场,获利润比只生产书桌多了48000元。
没派上用场,获利润比只生产书桌多了48000元。
③在第三个问题中,即怎样安排生产,可获利润最大?
![]() ,约束条件为
,约束条件为
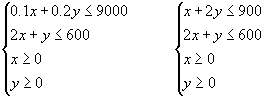
对此,我们用图解法求解,
先作出可行域,如图阴影部分。
![]()
![]() 时得直线
时得直线 ![]() 与
与 ![]() 平行的直线
平行的直线 ![]() 过可行域内的点M(0,600)。因为与
过可行域内的点M(0,600)。因为与 ![]() 平等的过可行域内的点的所有直线中,
平等的过可行域内的点的所有直线中, ![]() 距原点最远,所以最优解为
距原点最远,所以最优解为 ![]() ,即此时
,即此时 ![]()
因此,只生产书橱600张可获得最大利润,最大利润是72000元。
B.讨论
为什么会出现只生产书橱,可获最大利润的情形呢?第一,书橱比书桌价格高,因此应该尽可能多生产书橱;第二,生产一张书橱只需要五合板 ![]() ,生产一张书桌却需要五合板
,生产一张书桌却需要五合板 ![]() ,按家具厂五合板的存有量
,按家具厂五合板的存有量 ![]() ,可生产书橱600张,若同时又生产书桌,则生产一张书桌就要减少两张书橱,显然这不合算;第三,生产书橱的另种材料,即方木料是足够供应的,家具厂方木料存有量为
,可生产书橱600张,若同时又生产书桌,则生产一张书桌就要减少两张书橱,显然这不合算;第三,生产书橱的另种材料,即方木料是足够供应的,家具厂方木料存有量为 ![]() ,而生产600张书橱只需要方木料
,而生产600张书橱只需要方木料 ![]() 。
。
这是一个特殊的线性规划问题,再来研究它的解法。
C.改变这个例子的个别条件,再来研究它的解法。
将这个例子中方木料存有量改为 ![]() ,其他条件不变,则
,其他条件不变,则
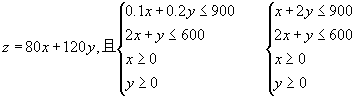
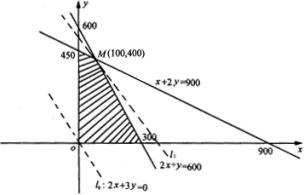 作出可行域,如图阴影部分,且过可行域内点M(100,400)而平行于
作出可行域,如图阴影部分,且过可行域内点M(100,400)而平行于 ![]() 的直线
的直线 ![]() 离原点的距离最大,所以最优解为(100,400),这时
离原点的距离最大,所以最优解为(100,400),这时 ![]() (元)。
(元)。
故生产书桌100、书橱400张,可获最大利润56000元。
总结、扩展
1.线性规划问题的数字模型。
2.线性规划在两类问题中的应用
布置作业
到附近的工厂、乡镇企业、商店、学校等作调查研究,了解线性规划在实际中的应用,或提出能用线性规划的知识提高生产效率的实际问题,并作出解答。把实习和研究活动的成果写成实习报告、研究报告或小论文,并互相交流。
探究活动
如何确定水电站的位置
小河同侧有两个村庄A,B,两村庄计划于河上共建一水电站发电供两村使用.已知 A,B两村到河边的垂直距离分别为300m和700m,且两村相距500m,问水电站建于何处,送电到两村电线用料最省?
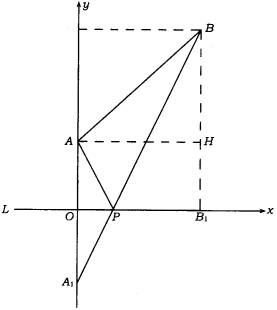 [解]视两村庄为两点A,B,小河为一条直线L,原问题便转化成在直线上找一点P,使P点到A,B两点距离之和为最小的问题.
[解]视两村庄为两点A,B,小河为一条直线L,原问题便转化成在直线上找一点P,使P点到A,B两点距离之和为最小的问题.
以L所在直线为 ![]() 轴,
轴, ![]() 轴通过A点建立直角坐标系,如图所示.作A关于
轴通过A点建立直角坐标系,如图所示.作A关于 ![]() 轴的对称点
轴的对称点 ![]() ,连
,连 ![]() ,
, ![]() 与
与 ![]() 轴交于点P.由平面几何知识得,点P即为所求.据已知条件,A(0,300),
轴交于点P.由平面几何知识得,点P即为所求.据已知条件,A(0,300), ![]() (0,-300).过B作
(0,-300).过B作 ![]() 轴于点
轴于点 ![]() ,过A作
,过A作 ![]() ,于点H.
,于点H.
由 ![]() ,
, ![]() ,得B(300,700).于是直线
,得B(300,700).于是直线 ![]() 的方程为
的方程为
![]()
即
![]()
所以P点的坐标即为 ![]() 与
与 ![]() 轴的交点(90,0),即水电站应建在河边两村间且离A村距河边的最近点90 m的地方
轴的交点(90,0),即水电站应建在河边两村间且离A村距河边的最近点90 m的地方
 打印本文
打印本文  关闭窗口
关闭窗口