 打印本文
打印本文  关闭窗口
关闭窗口 教学目标
(1)掌握圆的标准方程,能根据圆心坐标和半径熟练地写出圆的标准方程,也能根据圆的标准方程熟练地写出圆的圆心坐标和半径.
(2)掌握圆的一般方程,了解圆的一般方程的结构特征,熟练掌握圆的标准方程和一般方程之间的互化.
(3)了解参数方程的概念,理解圆的参数方程,能够进行圆的普通方程与参数方程之间的互化,能应用圆的参数方程解决有关的简单问题.
(4)掌握直线和圆的位置关系,会求圆的切线.
(5)进一步理解曲线方程的概念、熟悉求曲线方程的方法.
教学建议
教材分析
(1)知识结构
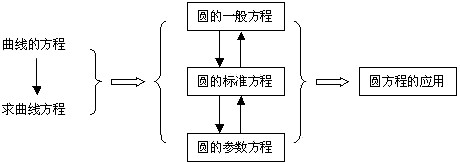
(2)重点、难点分析
①本节内容教学的重点是圆的标准方程、一般方程、参数方程的推导,根据条件求圆的方程,用圆的方程解决相关问题.
②本节的难点是圆的一般方程的结构特征,以及圆方程的求解和应用.
教法建议
(1)圆是最简单的曲线.这节教材安排在学习了曲线方程概念和求曲线方程之后,学习三大圆锥曲线之前,旨在熟悉曲线和方程的理论,为后继学习做好准备.同时,有关圆的问题,特别是直线与圆的位置关系问题,也是解析几何中的基本问题,这些问题的解决为圆锥曲线问题的解决提供了基本的思想方法.因此教学中应加强练习,使学生确实掌握这一单元的知识和方法.
(2)在解决有关圆的问题的过程中多次用到配方法、待定系数法等思想方法,教学中应多总结.
(3)解决有关圆的问题,要经常用到一元二次方程的理论、平面几何知识和前边学过的解析几何的基本知识,教师在教学中要注意多复习、多运用,培养学生运算能力和简化运算过程的意识.
(4)有关圆的内容非常丰富,有很多有价值的问题.建议适当选择一些内容供学生研究.例如由过圆上一点的切线方程引申到切点弦方程就是一个很有价值的问题.类似的还有圆系方程等问题.
教学设计示例
圆的一般方程
教学目标:
(1)掌握圆的一般方程及其特点.
(2)能将圆的一般方程转化为圆的标准方程,从而求出圆心和半径.
(3)能用待定系数法,由已知条件求出圆的一般方程.
(4)通过本节课学习,进一步掌握配方法和待定系数法.
教学重点:(1)用配方法,把圆的一般方程转化成标准方程,求出圆心和半径.
(2)用待定系数法求圆的方程.
教学难点:圆的一般方程特点的研究.
教学用具:计算机.
教学方法:启发引导法,讨论法.
教学过程:
【引入】
前边已经学过了圆的标准方程
![]()
把它展开得
![]()
任何圆的方程都可以通过展开化成形如
![]() ①
①
的方程
【问题1】
形如①的方程的曲线是否都是圆?
师生共同讨论分析:
如果①表示圆,那么它一定是某个圆的标准方程展开整理得到的.我们把它再写成原来的形式不就可以看出来了吗?运用配方法,得
![]() ②
②
显然②是不是圆方程与 ![]() 是什么样的数密切相关,具体如下:
是什么样的数密切相关,具体如下:
(1)当 ![]() 时,②表示以
时,②表示以 ![]() 为圆心、以
为圆心、以 ![]() 为半径的圆;
为半径的圆;
(2)当 ![]() 时,②表示一个点
时,②表示一个点 ![]() ;
;
(3)当 ![]() 时,②不表示任何曲线.
时,②不表示任何曲线.
总结:任意形如①的方程可能表示一个圆,也可能表示一个点,还有可能什么也不表示.
圆的一般方程的定义:
当 ![]() 时,①表示以
时,①表示以 ![]() 为圆心、以
为圆心、以 ![]() 为半径的圆,
为半径的圆,
此时①称作圆的一般方程.
即称形如 ![]() 的方程为圆的一般方程.
的方程为圆的一般方程.
【问题2】圆的一般方程的特点,与圆的标准方程的异同.
(1) ![]() 和
和 ![]() 的系数相同,都不为0.
的系数相同,都不为0.
(2)没有形如 ![]() 的二次项.
的二次项.
圆的一般方程与一般的二元二次方程
![]() ③
③
相比较,上述(1)、(2)两个条件仅是③表示圆的必要条件,而不是充分条件或充要条件.
圆的一般方程与圆的标准方程各有千秋:
(1)圆的标准方程带有明显的几何的影子,圆心和半径一目了然.
(2)圆的一般方程表现出明显的代数的形式与结构,更适合方程理论的运用.
【实例分析】
例1:下列方程各表示什么图形.
(1) ![]() ;
;
(2) ![]() ;
;
(3) ![]() .
.
学生演算并回答
(1)表示点(0,0);
(2)配方得 ![]() ,表示以
,表示以 ![]() 为圆心,3为半径的圆;
为圆心,3为半径的圆;
(3)配方得 ![]() ,当
,当 ![]() 、
、 ![]() 同时为0时,表示原点(0,0);当
同时为0时,表示原点(0,0);当 ![]() 、
、 ![]() 不同时为0时,表示以
不同时为0时,表示以 ![]() 为圆心,
为圆心, ![]() 为半径的圆.
为半径的圆.
例2:求过三点 ![]() ,
, ![]() ,
, ![]() 的圆的方程,并求出圆心坐标和半径.
的圆的方程,并求出圆心坐标和半径.
分析:由于学习了圆的标准方程和圆的一般方程,那么本题既可以用标准方程求解,也可以用一般方程求解.
解:设圆的方程为
![]()
因为 ![]() 、
、 ![]() 、
、 ![]() 三点在圆上,则有
三点在圆上,则有
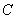
解得: ![]() ,
, ![]() ,
, ![]()
所求圆的方程为
![]()
可化为
![]()
圆心为 ![]() ,半径为5.
,半径为5.
请同学们再用标准方程求解,比较两种解法的区别.
【概括总结】通过学生讨论,师生共同总结:
(1)求圆的方程多用待定系数法.其步骤为:由题意设方程(标准方程或一般方程);根据条件列出关于待定系数的方程组;解方程组求出系数,写出方程.
(2)如何选用圆的标准方程和圆的一般方程.一般地,易求圆心和半径时,选用标准方程;如果给出圆上已知点,可选用一般方程.
下面再看一个问题: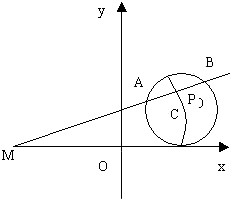
例3: 经过点 ![]() 作圆
作圆 ![]() 的割线,交圆
的割线,交圆 ![]() 于
于 ![]() 、
、 ![]() 两点,求线段
两点,求线段 ![]() 的中点
的中点 ![]() 的轨迹.
的轨迹.
解:圆 ![]() 的方程可化为
的方程可化为 ![]() ,其圆心为
,其圆心为 ![]() ,半径为2.设
,半径为2.设 ![]() 是轨迹上任意一点.
是轨迹上任意一点.
∵ ![]()
∴ ![]()
即
![]()
化简得
![]()
点 ![]() 在曲线上,并且曲线为圆
在曲线上,并且曲线为圆 ![]() 内部的一段圆弧.
内部的一段圆弧.
【练习巩固】
(1)方程 ![]() 表示的曲线是以
表示的曲线是以 ![]() 为圆心,4为半径的圆.求
为圆心,4为半径的圆.求 ![]() 、
、 ![]() 、
、 ![]() 的值.(结果为4,-6,-3)
的值.(结果为4,-6,-3)
(2)求经过三点 ![]() 、
、 ![]() 、
、 ![]() 的圆的方程.
的圆的方程.
分析:用圆的一般方程,代入点的坐标,解方程组得圆的方程为 ![]() .
.
(3)课本第79页练习1,2.
【小结】师生共同总结:
(1)圆的一般方程及其特点.
(2)用配方法化圆的一般方程为圆的标准方程,求圆心坐标和半径.
(3)用待定系数法求圆的方程.
【作业】课本第82页5,6,7,8.
【板书设计】
|
圆的一般方程 | |||
|
圆的一般方程 |
例1: 例2: |
例3: 练习: |
小结: 作业: |
 打印本文
打印本文  关闭窗口
关闭窗口