 打印本文
打印本文  关闭窗口
关闭窗口 教学目标
1.理解等差数列的概念,掌握等差数列的通项公式,并能运用通项公式解决简单的问题.
(1)了解公差的概念,明确一个数列是等差数列的限定条件,能根据定义判断一个数列是等差数列,了解等差中项的概念;
(2)正确认识使用等差数列的各种表示法,能灵活运用通项公式求等差数列的首项、公差、项数、指定的项;
(3)能通过通项公式与图像认识等差数列的性质,能用图像与通项公式的关系解决某些问题.
2.通过等差数列的图像的应用,进一步渗透数形结合思想、函数思想;通过等差数列通项公式的运用,渗透方程思想.
3.通过等差数列概念的归纳概括,培养学生的观察、分析资料的能力,积极思维,追求新知的创新意识;通过对等差数列的研究,使学生明确等差数列与一般数列的内在联系,从而渗透特殊与一般的辩证唯物主义观点.
关于等差数列的教学建议
(1)知识结构
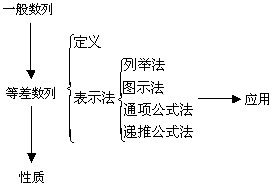
(2)重点、难点分析
①教学重点是等差数列的定义和对通项公式的认识与应用,等差数列是特殊的数列,定义恰恰是其特殊性、也是本质属性的准确反映和高度概括,准确把握定义是正确认识等差数列,解决相关问题的前提条件.通项公式是项与项数的函数关系,是研究一个数列的重要工具,等差数列的通项公式的结构与一次函数的解析式密切相关,通过函数图象研究数列性质成为可能.
②通过不完全归纳法得出等差数列的通项公式,所以是教学中的一个难点;另外, ![]() 出现在一个等式中,运用方程的思想,已知三个量可以求出第四个量.由于一个公式中字母较多,学生应用时会有一定的困难,通项公式的灵活运用是教学的有一难点.
出现在一个等式中,运用方程的思想,已知三个量可以求出第四个量.由于一个公式中字母较多,学生应用时会有一定的困难,通项公式的灵活运用是教学的有一难点.
(3)教法建议
①本节内容分为两课时,一节为等差数列的定义与表示法,一节为等差数列通项公式的应用.
②等差数列定义的引出可先给出几组等差数列,让学生观察、比较,概括共同规律,再由学生尝试说出等差数列的定义,对程度差的学生可以提示定义的结构:“……的数列叫做等差数列”,由学生把限定条件一一列举出来,为等比数列的定义作准备.如果学生给出的定义不准确,可让学生研究讨论,用符合学生的定义但不是等差数列的数列作为反例,再由学生修改其定义,逐步完善定义.
③等差数列的定义归纳出来后,由学生举一些等差数列的例子,以此让学生思考确定一个等差数列的条件.
④由学生根据一般数列的表示法尝试表示等差数列,前提条件是已知数列的首项与公差.明确指出其图像是一条直线上的一些点,根据图像观察项随项数的变化规律;再看通项公式,项 ![]() 可看作项数
可看作项数 ![]() 的一次型(
的一次型( ![]() )函数,这与其图像的形状相对应.
)函数,这与其图像的形状相对应.
⑤有穷等差数列的末项与通项是有区别的,数列的通项公式 ![]() 是数列第
是数列第 ![]() 项
项 ![]() 与项数
与项数 ![]() 之间的函数关系式,有穷等差数列的项数未必是
之间的函数关系式,有穷等差数列的项数未必是 ![]() ,即其末项未必是该数列的第
,即其末项未必是该数列的第 ![]() 项,在教学中一定要强调这一点.
项,在教学中一定要强调这一点.
⑥等差数列前 ![]() 项和的公式推导离不开等差数列的性质,所以在本节课应补充一些重要的性质;另外可让学生研究等差数列的子数列,有规律的子数列会引起学生的兴趣.
项和的公式推导离不开等差数列的性质,所以在本节课应补充一些重要的性质;另外可让学生研究等差数列的子数列,有规律的子数列会引起学生的兴趣.
⑦等差数列是现实生活中广泛存在的数列的数学模型,如教材中的例题、习题等,还可让学生去搜集,然后彼此交流,提出相关问题,自己尝试解决,为学生提供相互学习的机会,创设相互研讨的课堂环境.
等差数列通项公式的教学设计示例
教学目标
1.通过教与学的互动,使学生加深对等差数列通项公式的认识,能参与编拟一些简单的问题,并解决这些问题;
2.利用通项公式求等差数列的项、项数、公差、首项,使学生进一步体会方程思想;
3.通过参与编题解题,激发学生学习的兴趣.
教学重点,难点
教学重点是通项公式的认识;教学难点是对公式的灵活运用.
教学用具
实物投影仪,多媒体软件,电脑.
教学方法
研探式.
教学过程
一.复习提问
前一节课我们学习了等差数列的概念、表示法,请同学们回忆等差数列的定义,其表示法都有哪些?
等差数列的概念是从相邻两项的关系加以定义的,这个关系用递推公式来表示比较简单,但我们要围绕通项公式作进一步的理解与应用.
二.主体设计
通项公式 ![]() 反映了项
反映了项 ![]() 与项数
与项数 ![]() 之间的函数关系,当等差数列的首项与公差确定后,数列的每一项便确定了,可以求指定的项(即已知
之间的函数关系,当等差数列的首项与公差确定后,数列的每一项便确定了,可以求指定的项(即已知 ![]() 求
求 ![]() ).找学生试举一例如:“已知等差数列
).找学生试举一例如:“已知等差数列 ![]() 中,首项
中,首项 ![]() ,公差
,公差 ![]() ,求
,求 ![]() .”这是通项公式的简单应用,由学生解答后,要求每个学生出一些运用等差数列通项公式的题目,包括正用、反用与变用,简单、复杂,定量、定性的均可,教师巡视将好题搜集起来,分类投影在屏幕上.
.”这是通项公式的简单应用,由学生解答后,要求每个学生出一些运用等差数列通项公式的题目,包括正用、反用与变用,简单、复杂,定量、定性的均可,教师巡视将好题搜集起来,分类投影在屏幕上.
1.方程思想的运用
(1)已知等差数列 ![]() 中,首项
中,首项 ![]() ,公差
,公差 ![]() ,则-397是该数列的第______项.
,则-397是该数列的第______项.
(2)已知等差数列 ![]() 中,首项
中,首项 ![]() ,
, ![]() 则公差
则公差 ![]()
(3)已知等差数列 ![]() 中,公差
中,公差 ![]() ,
, ![]() 则首项
则首项 ![]()
这一类问题先由学生解决,之后教师点评,四个量 ![]() ,
, ![]() 在一个等式中,运用方程的思想方法,已知其中三个量的值,可以求得第四个量.
在一个等式中,运用方程的思想方法,已知其中三个量的值,可以求得第四个量.
2.基本量方法的使用
(1)已知等差数列 ![]() 中,
中, ![]()
![]() ,求
,求 ![]() 的值.
的值.
(2)已知等差数列 ![]() 中,
中, ![]() ,
, ![]() 求
求 ![]() .
.
若学生的题目只有这两种类型,教师可以小结(最好请出题者、解题者概括):因为已知条件可以化为关于 ![]() 和
和 ![]() 的二元方程组,所以这些等差数列是确定的,由
的二元方程组,所以这些等差数列是确定的,由 ![]() 和
和 ![]() 写出通项公式,便可归结为前一类问题.解决这类问题只需把两个条件(等式)化为关于
写出通项公式,便可归结为前一类问题.解决这类问题只需把两个条件(等式)化为关于 ![]() 和
和 ![]() 的二元方程组,以求得
的二元方程组,以求得 ![]() 和
和 ![]() ,
, ![]() 和
和 ![]() 称作基本量.
称作基本量.
教师提出新的问题,已知等差数列的一个条件(等式),能否确定一个等差数列?学生回答后,教师再启发,由这一个条件可得到关于 ![]() 和
和 ![]() 的二元方程,这是一个
的二元方程,这是一个 ![]() 和
和 ![]() 的制约关系,从这个关系可以得到什么结论?举例说明(例题可由学生或教师给出,视具体情况而定).
的制约关系,从这个关系可以得到什么结论?举例说明(例题可由学生或教师给出,视具体情况而定).
如:已知等差数列 ![]() 中,
中, ![]() …
…
由条件可得 ![]() 即
即 ![]() ,可知
,可知 ![]() ,这是比较显然的,与之相关的还能有什么结论?若学生答不出可提示,一定得某一项的值么?能否与两项有关?多项有关?由学生发现规律,完善问题
,这是比较显然的,与之相关的还能有什么结论?若学生答不出可提示,一定得某一项的值么?能否与两项有关?多项有关?由学生发现规律,完善问题
(3)已知等差数列 ![]() 中,
中, ![]() 求
求 ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;….
;….
类似的还有
(4)已知等差数列 ![]() 中,
中, ![]() 求
求 ![]() 的值.
的值.
以上属于对数列的项进行定量的研究,有无定性的判断?引出
3.研究等差数列的单调性
![]() ,考察
,考察 ![]() 随项数
随项数 ![]() 的变化规律.着重考虑
的变化规律.着重考虑 ![]() 的情况. 此时
的情况. 此时 ![]() 是
是 ![]() 的一次函数,其单调性取决于
的一次函数,其单调性取决于 ![]() 的符号,由学生叙述结果.这个结果与考察相邻两项的差所得结果是一致的.
的符号,由学生叙述结果.这个结果与考察相邻两项的差所得结果是一致的.
4.研究项的符号
这是为研究等差数列前 ![]() 项和的最值所做的准备工作.可配备的题目如
项和的最值所做的准备工作.可配备的题目如
(1)已知数列 ![]() 的通项公式为
的通项公式为 ![]() ,问数列从第几项开始小于0?
,问数列从第几项开始小于0?
(2)等差数列 ![]() 从第________项起以后每项均为负数.
从第________项起以后每项均为负数.
三.小结
1. 用方程思想认识等差数列通项公式;
2. 用函数思想解决等差数列问题.
四.板书设计
|
等差数列通项公式 1. 方程思想的运用
4. 研究项的符号 |
 打印本文
打印本文  关闭窗口
关闭窗口