圆、扇形、弓形的面积(一)

　　教学目标：

　　1、掌握扇形面积公式的推导过程，初步运用扇形面积公式进行一些有关计算；

　　2、通过扇形面积公式的推导，培养学生抽象、理解、概括、归纳能力和迁移能力；

　　3、在扇形面积公式的推导和例题教学过程中，渗透“从特殊到一般，再由一般到特殊”的辩证思想．

　　教学重点：扇形面积公式的导出及应用．

　　教学难点：对图形的分析．

　　教学活动设计：

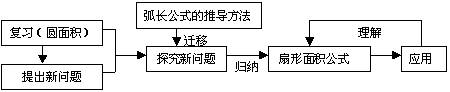
　　（一）复习（圆面积）

　　已知⊙O半径为R，⊙O的面积S是多少？

S=πR²

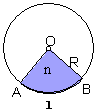
　　我们在求面积时往往只需要求出圆的一部分面积，如图中阴影图形的面积．为了更好研究这样的图形引出一个概念．

　　扇形：一条弧和经过这条弧的端点的两条半径所组成的图形叫做扇形．

　　提出新问题：已知⊙O半径为R，求圆心角n°的扇形的面积．

　　（二）迁移方法、探究新问题、归纳结论

　　1、迁移方法

　　教师引导学生迁移推导弧长公式的方法步骤：

　　（1）圆周长C=2πR；

　　（2）1°圆心角所对弧长= ；

　　（3）n°圆心角所对的弧长是1°圆心角所对的弧长的n倍；

　　（4）n°圆心角所对弧长= ．

　　归纳结论：若设⊙O半径为R， n°圆心角所对弧长l，则   （弧长公式）

　　2、探究新问题

　　教师组织学生对比研究：

　　（1）圆面积S=πR²；

　　（2）圆心角为1°的扇形的面积= ；

　　（3）圆心角为n°的扇形的面积是圆心角为1°的扇形的面积n倍；

　　（4）圆心角为n°的扇形的面积= ．

　　归纳结论：若设⊙O半径为R，圆心角为n°的扇形的面积S_扇形，则

S_扇形= （扇形面积公式）

　　（三）理解公式

　　教师引导学生理解：

　　（1）在应用扇形的面积公式S_扇形= 进行计算时，要注意公式中n的意义．n表示1°圆心角的倍数，它是不带单位的；

　　（2）公式可以理解记忆（即按照上面推导过程记忆）；

　　提出问题：扇形的面积公式与弧长公式有联系吗？（教师组织学生探讨）

S_扇形= lR

　　想一想：这个公式与什么公式类似？（教师引导学生进行，或小组协作研究）

　　与三角形的面积公式类似，只要把扇形看成一个曲边三角形，把弧长l看作底，R看作高就行了．这样对比，帮助学生记忆公式．实际上，把扇形的弧分得越来越小，作经过各分点的半径，并顺次连结各分点，得到越来越多的小三角形，那么扇形的面积就是这些小三角形面积和的极限．要让学生在理解的基础上记住公式．

　　（四）应用

　　练习：1、已知扇形的圆心角为120°，半径为2，则这个扇形的面积，S_扇=____．

　　2、已知扇形面积为 ，圆心角为120°，则这个扇形的半径R=____．

　　3、已知半径为2的扇形，面积为 ，则它的圆心角的度数=____．

　　4、已知半径为2cm的扇形，其弧长为 ，则这个扇形的面积，S_扇=____．

　　5、已知半径为2的扇形，面积为 ，则这个扇形的弧长=____．

　　（ ，2，120°， ， ）

　　例1、已知正三角形的边长为a，求它的内切圆与外接圆组成的圆环的面积．

　　学生独立完成，对基础较差的学生教师指导

　　（1）怎样求圆环的面积？

　　（2）如果设外接圆的半径为R，内切圆的半径为r， R、r与已知边长a有什么联系？

　　解：设正三角形的外接圆、内切圆的半径分别为R，r，面积为S₁、S₂．

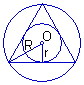　　S= ．

　　∵ ，∴S= ．

　　说明：要注意整体代入．

　　对于教材中的例2，可以采用典型例题中第4题，充分让学生探究．

　　课堂练习：教材P181练习中2、4题．

　　（五）总结

　　知识：扇形及扇形面积公式S_扇形= ，S_扇形= lR．

　　方法能力：迁移能力，对比方法；计算能力的培养．

　　（六）作业  教材P181练习1、3；P187中10．

此文章共有4页  第 1 2 3 4 页