 打印本文
打印本文  关闭窗口
关闭窗口 圆的认识
教学目标
1、使学生认识圆,知道圆的各部分名称。
2、使学生掌握圆的特征,理解和掌握在同一个圆里半径和直径的关系。
3、初步学会用圆规画圆,培养学生的作图能力。
4、培养学生观察、分析、抽象、概括等思维能力。
教学重点
理解和掌握圆的特征,学会用圆规画圆的方法。
教学难点
理解圆上的概念,归纳圆的特征。
教学过程
一、铺垫孕伏
1、教师用投影出示下面的图形:
![]()
提问:这是我们以前学过的哪些平面图形?这些图形都是由什么围成的?
教师指出:我们把这样的图形叫做平面上的直线图形。
2、(教师演示:一个小球,小球上还系着一段绳子,老师用手拽着绳子的一端,将小球甩起来)
提问:你们看小球画出了一个什么图形?(小球画出了一个圆)
教师:(出示铁丝围成的圆)这就是一个圆。圆也是一种平面图形,这节课我们就来学习圆的认识。(板书课题:圆的认识)
二、探究新知
1、教师让学生举例说明周围哪些物体上有圆。
2、认识圆的各部分名称和圆的特征。
(l)教师:请同学们拿出课前准备好的带有圆形的物体,借助这个物体自己动手在硬纸上画一个圆。
学生画完后,让他们把这个圆剪下来。
(2)教师:你们摸一摸圆的边缘,是直的还是弯的?(弯曲的)
教师说明:圆是平面上的一种曲线图形。
(3)教师:下面我们就通过具体操作,来认识一下圆的各部分名称和圆的特征。
①学生跟教师一起操作:先把圆对折、打开,换个方向,再对折,再打开……这样反复折几次。
教师提问:折过若干次后,你发现了什么?(在圆内出现了许多折痕)
仔细观察一下,这些折痕总在圆的什么地方相交?(圆的中心一点)
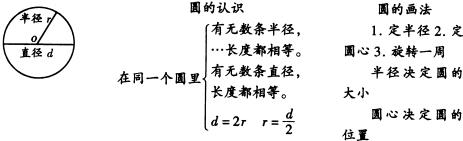
教师指出:我们把圆中心的这一点叫做圆心。圆心一般用字母 ![]() 表示。
表示。
(并板书:圆心 ![]() )
)
②教师:现在请同学们用尺子量一量圆心到圆上任意一点的距离,看一看,可以发现什么?(发现:圆心到圆上任意一点的距离都相等)
教师指出:我们把连接圆心和圆上任意一点的线段叫做半径,半径一般用字母 ![]() 表示。(教师在圆内画出一条半径,并板书:半径
表示。(教师在圆内画出一条半径,并板书:半径 ![]() )
)
教师提问:根据半径的概念同学们想一想,半径应具备哪些条件?
在同一个圆里可以画多少条半径?
所有半径的长度都相等吗?
启发学生说出:在同一个园里有无数条半径,所有半径的长度都相等。(板书)
③教师:同学们接着观察,刚才我们把圆对折时,每条折痕都从圆的什么地方通过?两端都在圆的什么地方?
教师指出:我们把通过圆心并且两端都在圆上的线段叫做直径。直径一般用字母 ![]() 来表示。(教师在圆内画出一条直径,并板书:直径
来表示。(教师在圆内画出一条直径,并板书:直径 ![]() )
)
教师提问:根据直径的概念同学们想一想,直径应具备什么条件?
在同一个圆里可以画出多少条直径?
自己用尺子量一量同一个圆里的几条直径,看一看,所有直径的长度都相等吗?
引导学生得出:在同一个圆里有无数条直径,所有直径的长度都相等。(板书)
④小结:通过刚才的学习我们知道,在同一个圆里有无数条半径,所有半径的长度都相等;有无数条直径,所有直径的长度也都相等。那么,在同一个圆里,直径的长度与半径的长度又有什么关系呢?(组织学生讨论)
引导学生得出:在同一个圆里,直径的长度是半径的2倍。
教师:如何用字母表示这种关系?(教师板书: ![]() )
)
教师:反过来,在同一个圆里,半径的长度是直径的几分之几?(教师板书: ![]() )
)
教师:这就是说,在同一个圆里,知道了半径的长度,乘2就可以求出直径的长度;知道了直径的长度,乘 ![]() 就可以求出半径的长度。
就可以求出半径的长度。
(4)阅读课本85-86页的内容,并勾画出重点。
3.反馈练习。
(1)用彩色笔标出下面各圆的半径和直径

(2)填表。
|
r(米) |
0.24 |
1.42 |
2.6 | ||
|
d(米) |
0.86 |
1.04 |
4.圆的画法。
教师:根据圆心到圆上任意一点的距离都相等这一特征,我们可以用圆规来画圆。
(1)学生自学
(2)教师示范画圆。
(3)教师归纳板书:1.定半径;2.定圆心;3.旋转一周。
教师强调:画圆时,圆规两脚间的距离不能改变,有针尖的一脚不能移动,旋转时要把重心放在有针尖的一脚。
(4)学生练习
(5)教师提问:为什么同学们画的圆不一样呢?
什么决定圆的大小?
什么决定圆的位置?
(半径决定圆的大小,圆心决定圆的位置)
(6)思考:体育课上,老师想在操场画一个大圆圈做游戏,没有这么大的圆规怎么办?
三、全课小结
这节课我们学习了什么?通过这节课的学习你有什么收获?
四、课堂练习
l、判断
(l)画圆时,圆规两脚间的距离是半径的长度。( )
(2)两端都在圆上的线段,叫做直径。( )
(3)圆心到圆上任意一点的距离都相等。( )
(4)半径2厘米的圆比直径3厘米的圆大。( )
(5)所有圆的半径都相等。( )
(6)在同一个圆里,半径是直径的 ![]() 。( )
。( )
(7)在同一个圆里,所有直径的长度都相等。( )
(8)两条半径可以组成一条直径。( )
五、课后作业
练习二十二 4、5、6
六、板书设计
 打印本文
打印本文  关闭窗口
关闭窗口