 打印本文
打印本文  关闭窗口
关闭窗口 解简易方程(一)
教学目标
1.使学生初步理解“方程”“方程的解”和“解方程”的含义。
2.初步掌握解简易方程的方法并会检验。
教学重点
使学生初步掌握解方程的方法和书写格式。
教学难点
帮助学生建立“方程”的概念,并会应用。
教学步骤
一、铺垫孕伏
1、口算下面各题
![]()
![]()
2、写出下面各题的式子
(1)一个足球 ![]() 元,3个足球多少元?
元,3个足球多少元?
(2) ![]() 减3的差。
减3的差。
二、探究新知
(一)教学方程的意义
1、出示天平:(教师向学生介绍)这是一架天平、可以用来称物品的重量。当天平的指针指在标尺中间时,表示天平平衡,即天平两端的重量相等。
2、介绍等式:在天平的两边上重量相等的物体,左边放20克砝码和30克砝码,右边
放50克砝码。请学生观察。
教师提问:这个天平平衡吗?说明了什么?谁会用等式表示?
(这时天平平衡,说明了天平左右两边的重量相等,等式为 ![]() )
)
教师说明:这是一个等式,等号的左边和右边相等。
3、引出方程。(改变天平上的物品和砝码)
教师提问:请同学们观察,天平平衡说明了什么?怎样用式子表示,请同学们试一试。( ![]() )
)
教师说明:这个未知数“?”,如果用 ![]() 来表示就可以写成
来表示就可以写成 ![]() 。
。
教师提问:这个等式和上面的等式有什么不同?(这个等式含有未知数“ ![]() ”)
”)
4、列出含有未知数的等式:(出示第三幅图)
教师提问:
(1)这幅图是什么意思?
(2)每个篮球的价钱是 ![]() 元,3个篮球多少元,怎样用式子表示?(3
元,3个篮球多少元,怎样用式子表示?(3 ![]() )
)
(3)3个篮球是234元,怎样用含有未知数的等式表示?
教师板书: ![]()
5、总结方程的意义。
教师提问:观察上面三个等式回答问题。这三个等式有什么相同点和不同点?
相同点:都是相等的式子。
不同点:第一个等式不含有未知数,第二个和第三个等式含有未知数
教师板书:象这种含有未知数的等式,叫方程.
6、举例说明什么叫方程。
强调两点:一:含有未知数
二:等式
7、方程与等式的联系与区别,方程与等式之间是什么关系呢?(学生讨论)
小结:所有的方程都是等式,所有的等式不一定都是方程,含有未知数的等式是方程,不含未知数的等式不是方程。
(二)教学方程的解和解方程
1、教师提问:在 ![]() 中,
中, ![]() 等于多少时方程左边和右边相等?
等于多少时方程左边和右边相等?
( ![]() 时方程左边和右边相等)
时方程左边和右边相等)
在 ![]() 中,
中, ![]() 等于多少时方程的左边和右边相等?
等于多少时方程的左边和右边相等?
( ![]() 时方程的左边和右边相等)
时方程的左边和右边相等)
2、教师引导:使方程左右两边相等的未知数的值,叫做方程的解。
谁是方程 ![]() 的解?(
的解?( ![]() 是方程
是方程 ![]() 的解)
的解)
谁是方程 ![]() 的解?(
的解?( ![]() 是方程
是方程 ![]() 的解)
的解)
3、30是上面方程的解吗?为什么?
(30不是上面方程的解,因为它不能使方程左右两边相等)
4、引导学生说明: ![]() ,
, ![]() 是怎样求出来的?
是怎样求出来的?
教师板书:求方程的解的过程叫做解方程。
5、例1 解方程 ![]() -8=16
-8=16
教师提问:
(1)解方程先写什么?等号怎样写?(先写解,等号要对齐)
(2)根据什么计算?
(3)怎样检查解方程是否正确?
教师板书:
解:根据被减数等于减数加差
![]()
![]()
检验:把 ![]() 代入原方程,
代入原方程,
左边 ![]() ,右边
,右边 ![]()
左边=右边
所以 ![]() 是原方程的解。
是原方程的解。
6、讨论:“方程的解”和“解方程”有什么区别?
三、课堂小结
今天你学到了哪些知识?什么叫方程?方程的解和解方程有什么区别?
四、巩固练习
1、填空
(1)含有未知数的( )叫做方程。
(2)使方程左右两边相等的( ),叫做方程的解。
(3)求方程的解的( )叫解方程。
(4)下面的式了中是等式的有( );
是方程的有( )。
![]()
![]()
![]()
![]()
![]()
![]()
2、判断,对的在括号里打√,错的打×。
(1)等式都是方程。( )
(2)方程都是等式。( )
(3) ![]() 是方程
是方程 ![]() 的解。( )
的解。( )
(4) ![]() 也是方程。( )
也是方程。( )
3、选择正确答案填在括号内
(1) ![]() 的解是( )
的解是( )
![]() ,
, ![]()
(2) ![]() 的解是( )
的解是( )
![]() ,
, ![]()
(3) ![]() 这个式子是( )
这个式子是( )
是方程 是等式 既是方程又是等式
(4) ![]() 是方程( )的解
是方程( )的解
![]()
![]()
五、布置作业
练习二十四4题。
六、板书设计
解简易方程
含有未知数的等式叫做方程。 例方程左右两边相等的未知数的值,叫做方程的解。
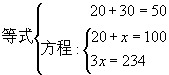 求方程的解的过程叫做解方程。
求方程的解的过程叫做解方程。
例1 解方程 ![]()
解:根据被减数等于减数加差
![]()
![]()
检验:把 ![]() 代入原方程,左边
代入原方程,左边 ![]() ,右边
,右边 ![]() ,所以
,所以 ![]() 是原方程的解。
是原方程的解。
 打印本文
打印本文  关闭窗口
关闭窗口